1) в одной из двух данных плоскостей, например Σ, строится линия уровня,
например h(h1, h2 ), где h2 // х;
2) введением новой системы плоскостей проекций П1 , П4 с осью x1 ^ h1 и П4 ^ h
строятся на П4 дополнительные проекции плоскостей – В4С4 для Σ и ΔK4M4L4 для
плоскости Δ;
3) отмечаются отрезки 1424 и 1121 – дополнительные проекции линии t(1121,1424)) пересечения заданных плоскостей;
4) в каждой из плоскостей Σ и Δ выбирается по одной точке, например, А Î Σ и
К Î Σ;
5) введением новой системы плоскостей проекций П4 , П5 с осью x2 // 1424 и
П5 // t(1,2) строятся на П5 дополнительные проекции 1525 , А5 , К5 фигур – линии
пересечения t (1, 2) и точек А, К;
6) введением новой системы плоскостей проекций П5 , П6 с осью x3 ^ 1525 и
П6 ^ t(1,2) строится на П6 линейный угол a двугранного угла ΣtΔ, который и
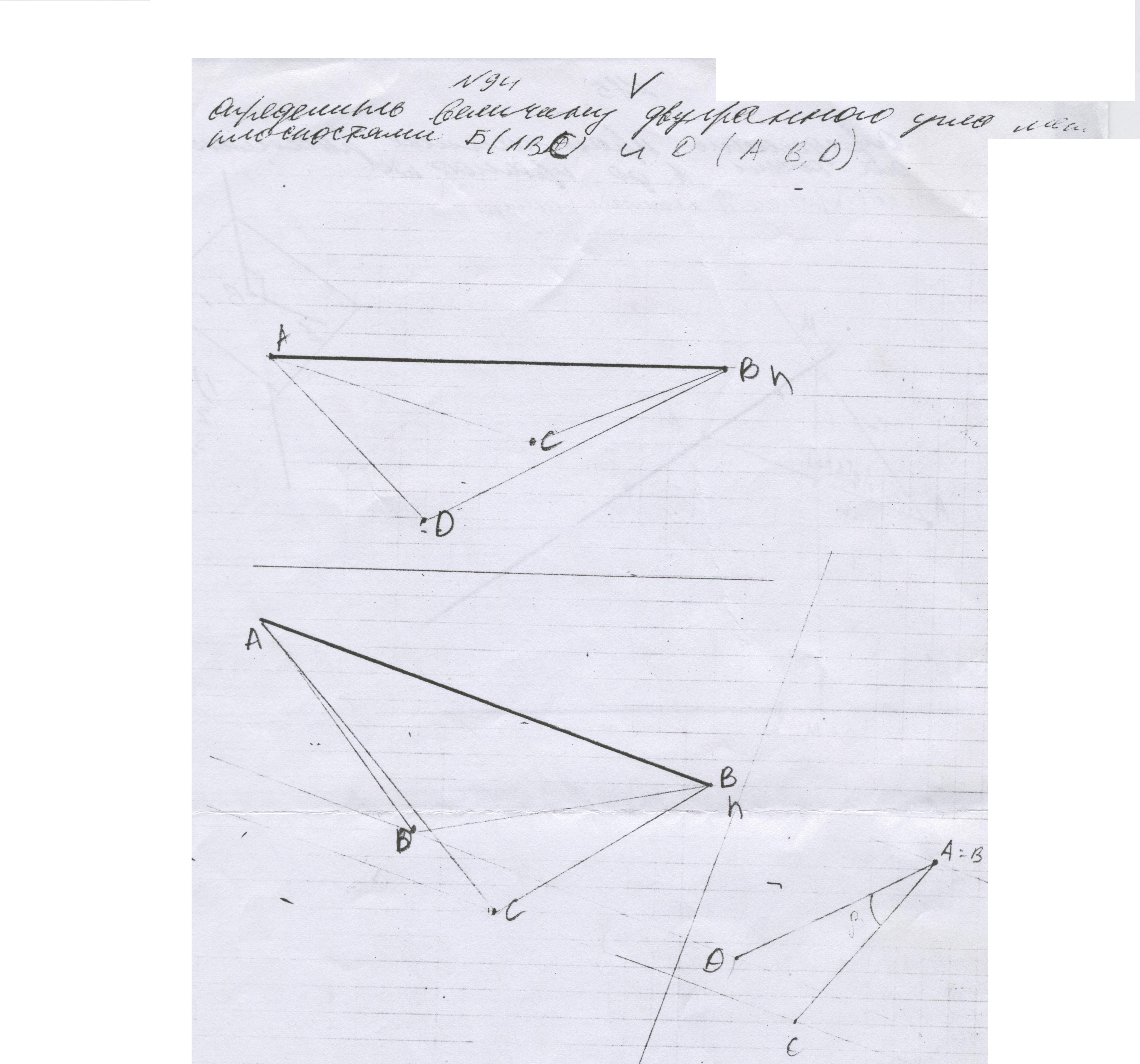
является решением задачи.Определить величину двугранного угла между плоскостями Б и Д
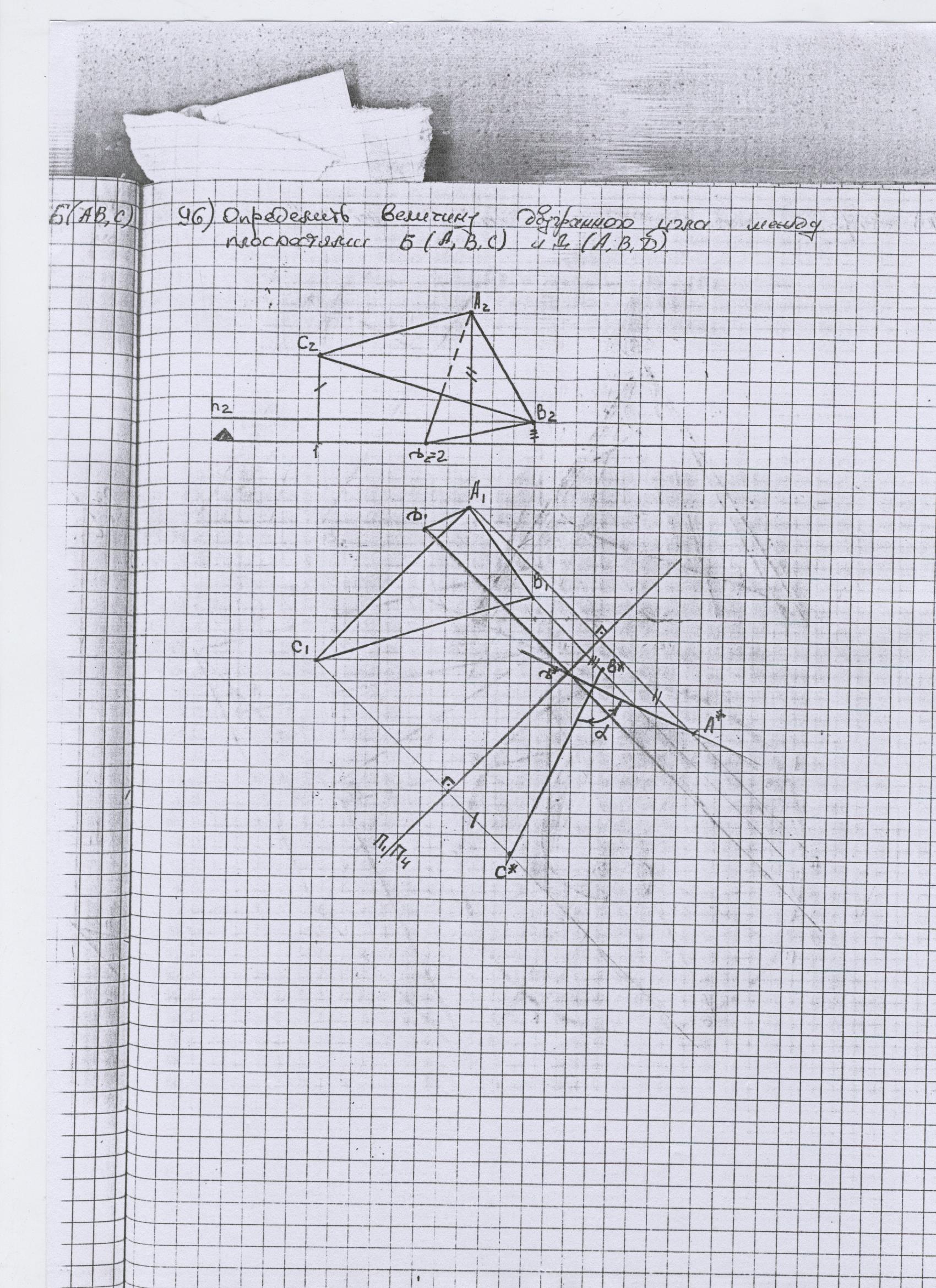Определить величину двугранного угла между плоскостями Б и Д.
