|
Пример 1
|
||||||
|
Вычислить двойной интеграл
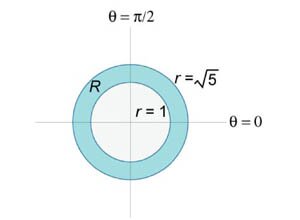
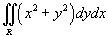 , преобразовав его в полярные координаты. Область интегрирования R представляет собой сектор , преобразовав его в полярные координаты. Область интегрирования R представляет собой сектор 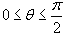 круга радиусом круга радиусом 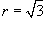 . .
Решение. 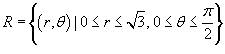 (рисунок 4). Применяя формулу (рисунок 4). Применяя формулу
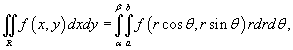 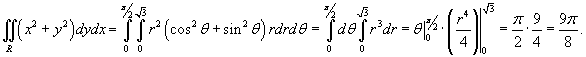 |
||||||
|
Пример 2
|
||||||
|
Вычислить интеграл
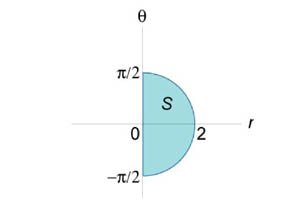
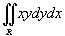 , в котором область интегрирования R представляет собой кольцо, ограниченное окружностями , в котором область интегрирования R представляет собой кольцо, ограниченное окружностями 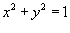 и и 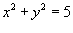 . .
Решение. 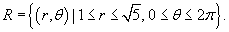
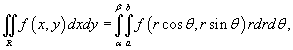 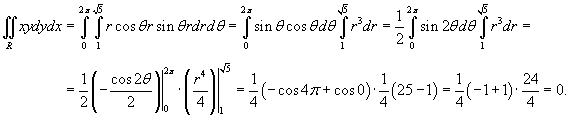 |
||||||
|
Пример 3
|
||||||
|
Найти интеграл
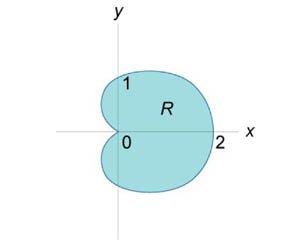
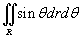 , где область интегрирования R ограничена кардиоидой , где область интегрирования R ограничена кардиоидой 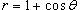 (рисунок 6). (рисунок 6).
Решение. 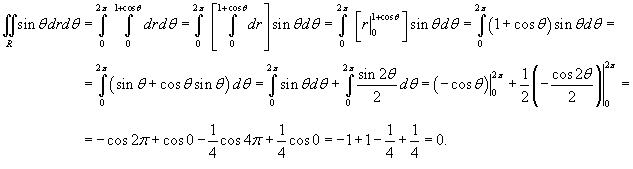 |
||||||
|
Пример 4
|
||||||
|
Вычислить интеграл
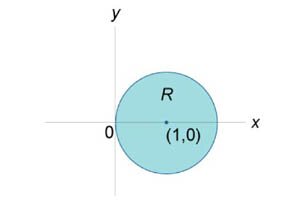
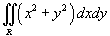 в круге в круге 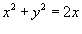 . .
Решение.
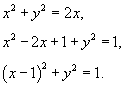 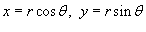 , найдем уравнение окружности в полярных координатах. , найдем уравнение окружности в полярных координатах.
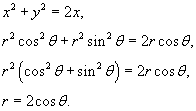 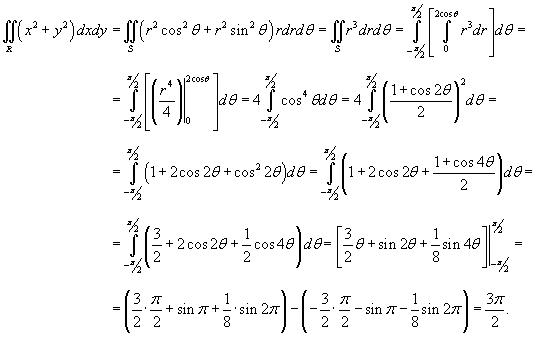 |
||||||
|
Пример 5
|
||||||
|
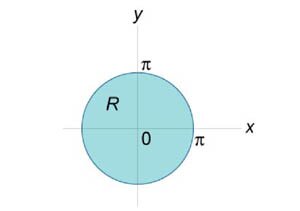
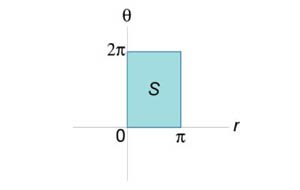
Вычислить двойной интеграл
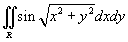 посредством преобразования в полярные координаты. Область интегрирования R представляет собой круг x2 + y2 ≤ π2. посредством преобразования в полярные координаты. Область интегрирования R представляет собой круг x2 + y2 ≤ π2.
Решение.
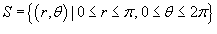 и показан на рисунке 10. Запишем исходный двойной интеграл в полярных координатах. и показан на рисунке 10. Запишем исходный двойной интеграл в полярных координатах.
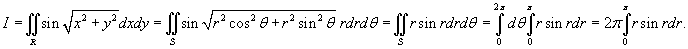 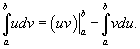 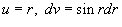 . Тогда . Тогда 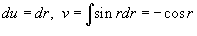 . Следовательно, . Следовательно,
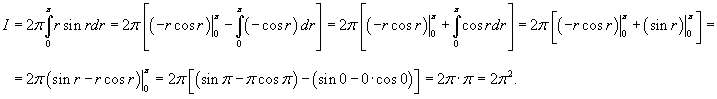 |
 |
|
||||||
Полярные
|
|||||||
|
|||||||