|
Если вещественная функция, непрерывная на отрезке |
Доказательство
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.
Геометрический смысл
Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.
Следствие
Если дифференцируемая функция обращается в ноль в  различных точках, то ее производная обращается в ноль по крайней мере в
различных точках, то ее производная обращается в ноль по крайней мере в  различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
Ещё одно следствие
Дифференцируемая функция на отрезке между двумя своими точками имеет касательную, параллельную секущей/хорде, проведённой через эти две точки.


![[a; b]](https://upload.wikimedia.org/math/9/4/a/94acf62f087ab3268b2b3fa5a8a7a79c.png) и
и 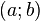 , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой
, принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой