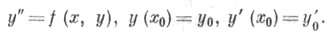
При интегрировании по сетке с постоянным шагом xn=x0+nh, n=1, 2, . . ., расчетные формулы имеют вид:
а) экстраполяционные:
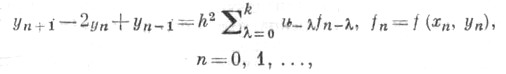
или (в разностной форме) 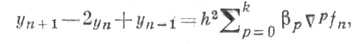
где 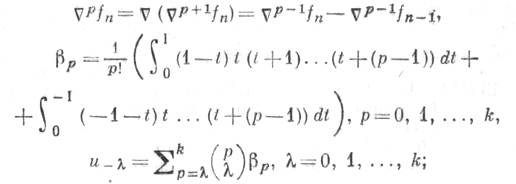
б) интерполяционные: 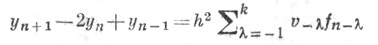
или (в разностной форме) 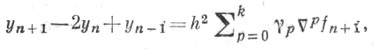
где 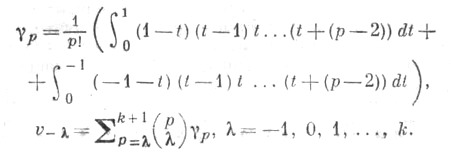
Первые значения коэффициентов 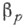 и
и 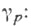
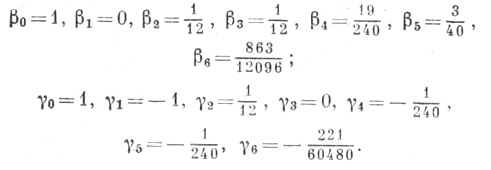
При одном и том же kформула б) точнее, но требует решения нелинейной системы уравнений длянахождения значения у п+1. На практике сначала находят приближенное значение решения yn+1 по формулеа), а затем проводят два-три уточнения но формуле 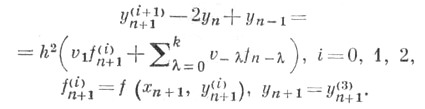
Применение Ш. м. предполагает, что уже известны приближенные значения решения в первых kузлах сетки:у 0, y1, . . ., у k (опорные значения). Эти значения вычисляют по Рунге - Кутта методу, либо используяразложение решения по формуле Тейлора. Необходимость использования специальных формул длявычисления значений в начале счета и в случае изменения шага сетки, по к-рой ведется интегрирование, приводит к существенному усложнению расчетных программ на ЭВМ.
Формулы Ш. м. с kчленами в правой части имеют погрешность порядка О(hk+1). Оценка погрешностианалогична соответствующей оценке для Адамса метода. Можно показать, что для любого kсуществуютустойчивые формулы с погрешностью порядка О(hk+1).
На практике обычно используются формулы с k=4, 5, 6. Широко используется Нумерова метод, принадлежащий к семейству интерполяционных Ш. м.:
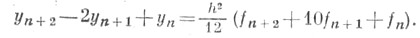
Метод предложен К. Штёрмером (С. Stermer, 1920).

