Рассмотрим дифференциальное уравнение
, (10)
где 
- вещественные постоянные, f(x) – известная функция. Общее решение неоднородного уравнения 
представляет собой сумму общего решения однородного уравнения 
и частного решения неоднородного уравнения 
, т.е. 
.
Метод нахождения общего решения однородного уравнения с постоянными коэффициентами (8) подробно рассмотрен в предыдущем пункте. Для уравнения с постоянными коэффициентами, правые части которых имеют специальный вид, существует способ нахождения частного решения, который называется методом подбора форм частного решения.
Правая часть уравнения (10) f(x)=
(x) – многочлен n-й степени. В этом случае частное решение следует искать в виде 
, где
- многочлен той же степени, что и многочлен 
, но с неизвестными коэффициентами, а
- число корней характеристического уравнения, равных 0.
Метод неопределенных коэффициентов применяют при интегрировании рациональных дробей.
метод неопределенных коэффициентов,
суть которого состоит в следующем:
-
правую часть записанного равенства приводим к общему знаменателю, который совпадает со знаменателем дроби, стоящей в левой части этого равенства -
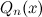, в числителе левой части получим некоторый многочлен 
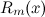с неизвестными коэффициентами; -
используем тот факт, что две дроби равны, когда равны их числители и знаменатели. Из того, что знаменатели левой и правой частей равенства равны, то значит, равны и числители:
-
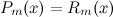
два многочлена равны, если равны коэффициенты при соответствующих степенях переменной, поэтому приравниваем коэффициенты при одинаковых степенях переменной
. В результате получаем систему для определения неизвестных коэффициентов.
