9 билет(5)

Бесконечно малая величина

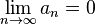Последовательность $a_n$ называется бесконечно малой, если $lim_{ntoinfty}a_n=0$ . Например, последовательность чисел $a_n=frac{1}{n}$ — бесконечно малая.

Функция называется бесконечно малой в окрестности точки $x_0$ , если $lim_{xto x_0}f(x)=0$ .

Функция называется бесконечно малой на бесконечности, если $lim_{xto+infty}f(x)=0$ либо $lim_{xto-infty}f(x)=0$ .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если $lim_{xto+infty}f(x)=a$ , то $f(x)-a=alpha(x)$ , $lim_{xto+infty}(f(x)-a)=0$ .

О п р е д е л е н и е. Бесконечно малые величины и называются эквивалентными, если предел их отношения равен единице:

Обозначается .