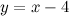1. Написать уравнение касательной к графику функции 
в точке 
.
а) Найдем значение функции в точке .
.
б) Найдем значение производной в точке . Сначала найдем производную функции 
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим: 
Ответ: .
2 Найти абсциссы точек, в которых касательные к графику функции 
параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси 
равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.
а) Найдем производную функции .
б) Приравняем производную к нулю и найдем значения 
, в которых касательная параллельна оси :
Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3.Найти асимптоты графика функции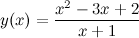 
Решение. Область определения функции:
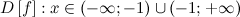
а) вертикальные асимптоты: прямая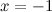 
- вертикальная асимптота, так как
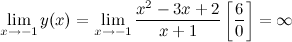
б) горизонтальные асимптоты: находим предел функции на бесконечности:
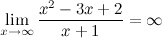
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты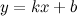 
:
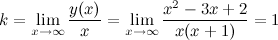
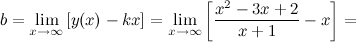
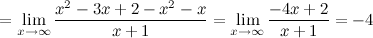
Таким образом, наклонная асимптота: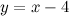 
.
Ответ. Вертикальная асимптота - прямая .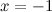
Наклонная асимптота - прямая
