Вопрос 29. Модуль вектора. Направляющие косинусы вектора. Условие коллинеарности векторов.

Определение направляющих косинусов

Направляющие косинусы однозначно задают направление вектора.

Соответственно координатам единичного вектора равны его направляющим косинусам.

Формулы вычисления направляющих косинусов вектора

Формула вычисления направляющих косинусов вектора для плоских задач

В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {a_x ; a_y} можно найти воспользовавшись следующей формулой

Свойство:

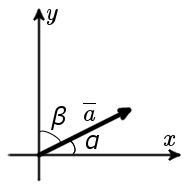рис. 1

Формула вычисления направляющих косинусов вектора для пространственных задач

В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {a_x ; a_y ; a_z} можно найти воспользовавшись следующей формулой

Свойство:

cos² α + cos² β + cos² γ = 1

Вектора, параллельные одной прямой или лежащие на одной прямой называютколлинеарными векторами (рис. 1).

рис. 1

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
 

a = n · b

Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

 

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = {a_x; a_y; a_z} и b = {na_x; na_y; na_z}. Найдем их векторное произведение

a × b =	i	j	k	= i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
	ax	ay	az
	bx	by	bz

= i (a_yna_z - a_zna_y) - j (a_xna_z - a_zna_x) + k (a_xna_y - a_yna_x) = 0i + 0j + 0k = 0