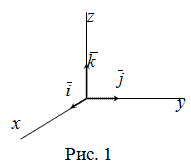
Разложение вектора по ортам координатных осей
Система ортов (или базисная система векторов) - это системаединичных векторов осей координат.
Орт координатной оси 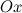 обозначается через
обозначается через 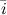 , оси
, оси 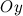 - через
- через 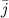 , оси
, оси 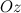 - через
- через 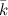 (рис. 1).
(рис. 1).
Для любого вектора 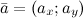 , который лежит в плоскости
, который лежит в плоскости 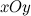 , имеет место следующее разложение:
, имеет место следующее разложение: 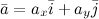
Если вектор 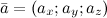 расположен в пространстве, то разложение по ортам координатных осей имеет вид:
расположен в пространстве, то разложение по ортам координатных осей имеет вид: 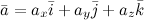
|
Рассмотрим координатную прямую с началом координат в точке О и единичным вектором i. Тогда для любого вектора aна этой прямой: a = axi. Свойство 1. При сложении векторов на оси их координаты складываются. Пусть вектор a = AB, где A и B - точки на оси с координатами xA и xB, соответственно. Тогда координата вектора a на оси равна разности координат его конца и его начала: ax = xB - xA. После того как определена координата вектора на координатной оси, координаты вектора на плоскости или в пространстве вводятся единообразно: вектор раскладывается на составляющие по координатным осям пары (для плоскости) или тройки (для пространства) координат этих составляющих и называются координатами вектора на плоскости или в пространстве. |
|
|
Для вычисления координат вектора используются два способа.
|