Наибольшее и наименьшее значение функции, непрерывной на отрезке

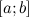Если функция  определена и непрерывна на отрезке  , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение  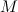функция  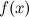принимает в точке 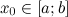, то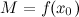 будет локальным максимумом функции 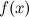, так как в этом случае существует окрестность точки 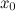, такая, что  .

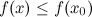Однако свое наибольшее значение 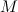 функция  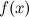может принимать и на концах отрезка  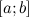. Поэтому, чтобы найти наибольшее значение  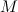непрерывной на отрезке  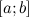функции 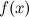, надо найти все максимумы функции на интервале 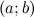и значения  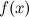на концах отрезка 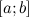, то есть  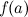и 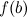, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.

Наименьшим значением 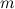 непрерывной на отрезке  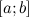функции  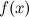будет наименьший минимум среди всех минимумов функции  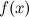на интервале  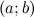и значени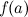й  и 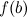.