Дифференциалы высших порядков
Пусть функция  зависит от переменной
зависит от переменной  и дифференцируема в точке
и дифференцируема в точке  . Может оказаться, что в точке
. Может оказаться, что в точке  дифференциал
дифференциал 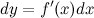 , рассматриваемый как функция от
, рассматриваемый как функция от  , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала
, есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 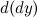 данной функции, который называетсядифференциалом второго порядка функции
данной функции, который называетсядифференциалом второго порядка функции  . Дифференциал второго порядка обозначается следующим образом:
. Дифференциал второго порядка обозначается следующим образом:
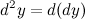
Аналогично определяются дифференциалы более высоких порядков.
Дифференциалом 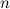 -го порядка
-го порядка 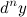 функции
функции  называется дифференциал от дифференциала
называется дифференциал от дифференциала 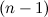 -го порядка этой функции, то есть
-го порядка этой функции, то есть
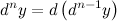
Производные высших порядков. Механический смысл второй производной. Пусть у=f(x) дифференцируема на всей области определения, производная 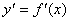 , от функции у=f(x) назпроизводной. Часто случается что
, от функции у=f(x) назпроизводной. Часто случается что 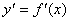 является дифференцируемой ф-цией от х, тогда производная от первой производной наз второй производной или производной второго порядка иобознач
является дифференцируемой ф-цией от х, тогда производная от первой производной наз второй производной или производной второго порядка иобознач 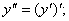
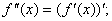
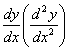 . Производная от второй производной ф-ции y=f(x), если она существует наз производной третьего порядка или третьей производной и обозначается
. Производная от второй производной ф-ции y=f(x), если она существует наз производной третьего порядка или третьей производной и обозначается 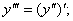
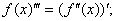
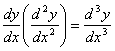 . Опр.производная n-порядка или n-производной, ф-ции y=f(x), если она сущ наз производной от производной n-1 порядка и обознач,
. Опр.производная n-порядка или n-производной, ф-ции y=f(x), если она сущ наз производной от производной n-1 порядка и обознач, 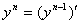 ;
; 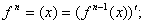
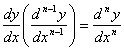 . Мех смысл 2ой произв. Пусть материальная точка движется прямолинейно по закону S=f(t) тогда скорость движения в момент времени t определяется по формуле
. Мех смысл 2ой произв. Пусть материальная точка движется прямолинейно по закону S=f(t) тогда скорость движения в момент времени t определяется по формуле 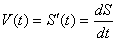 . В свою очередь скорость V(t) то же есть функция от времени t тогда производная
. В свою очередь скорость V(t) то же есть функция от времени t тогда производная 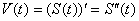 , если она существует определяет скорость изменения, скорости материальной точки движущейся по закону, но скорость ускорения скорости, называется ускорением и обозначается а(t). Таким образом ускорение а(t) прямолинейного движения материальной точки в момент времени t равно одной производной от скорости по времени или второй производной от пути по времени т.е.
, если она существует определяет скорость изменения, скорости материальной точки движущейся по закону, но скорость ускорения скорости, называется ускорением и обозначается а(t). Таким образом ускорение а(t) прямолинейного движения материальной точки в момент времени t равно одной производной от скорости по времени или второй производной от пути по времени т.е. 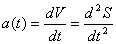 .
.

