Пусть функция 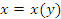 является обратной для функции
является обратной для функции 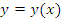 . Если существует отличная от нуля производная функции
. Если существует отличная от нуля производная функции 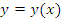 по переменной x, то существует и производная обратной функции
по переменной x, то существует и производная обратной функции 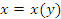 по переменной y. При этом
по переменной y. При этом
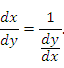
Доказательство. По определению производной
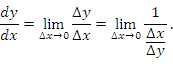
Согласно теореме о непрерывности дифференцируемых функциях, 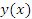 является непрерывной функцией и, следовательно,
является непрерывной функцией и, следовательно, 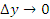 при ∆x → 0. Тогда
при ∆x → 0. Тогда
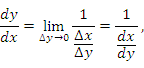
что влечет за собой доказываемое утверждение.
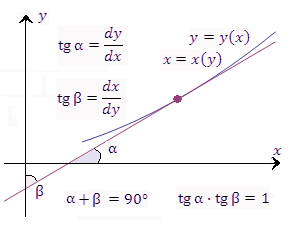
Производная обратной функции = обратной величине производной данной функции

