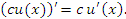1.Если существуют производные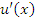 
и 
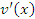, то производная от суммы (разности) функци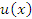й 
и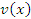 
равна сумме (разности) производных:
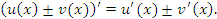
2.Если существуют производные 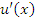и 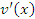, то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
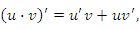
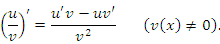
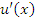и 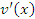, то выполняются следующие правила дифференцирования произведения функций и частного от их деления:
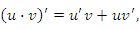
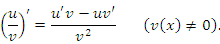
3. Постоянный множитель С можно выносить за знак производной:
