Пусть функции φ1,…,φn определены в некоторой окрестности точки x0∈Rm и непрерывны в точке x0, а функция f(y)=f(y1,…,yn)определена в окрестности точки y0=(φ1(x0),…,φn(x0)) и непрерывна в точке y0. Тогда в некоторой окрестности точки x0 определена сложная функция. Φ(x)=f(φ1(x),…,φn(x))причем функция Φ(x) непрерывна в точке x0.
Воспользуемся доказательством в случае одной переменной.

Теорема о непрерывности сложной функций

Пусть функция φ(t) непрерывна в точке t0 и функция f(x) непрерывна в точке x0=φ(t0). Тогда функция f(φ(t)) непрерывна в точке t0.

Доказательство:

Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем:
f(x) непрерывна в x0 ∀ε>0,∃δ∀x|x−x0|<δ  |f(x)−f(x0)|<ε ψ(e)непрерывна в t0 ∀δ>0∃η∀t |t−t0|<η|φ(t)−φ(t0)|<δ Выписывая  кванторы, получим, что:

Непрерывность элементарных функций

1. f(x) = C, (где С – постоянная) непрерывна на R, т.к. 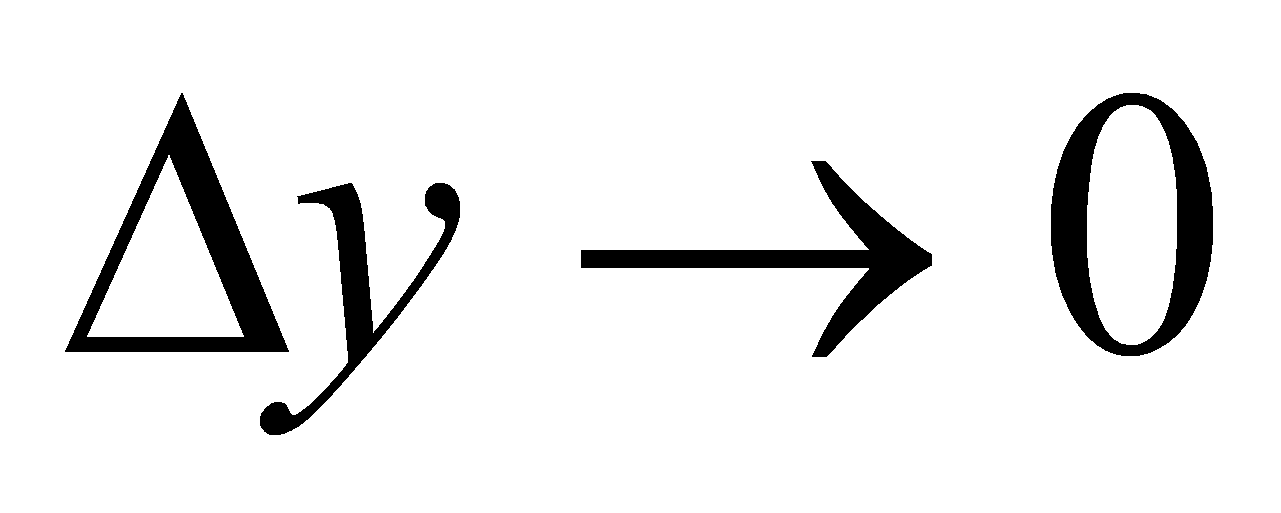 при любом x.

2. f(x) = x, непрерывна на R, т.к. 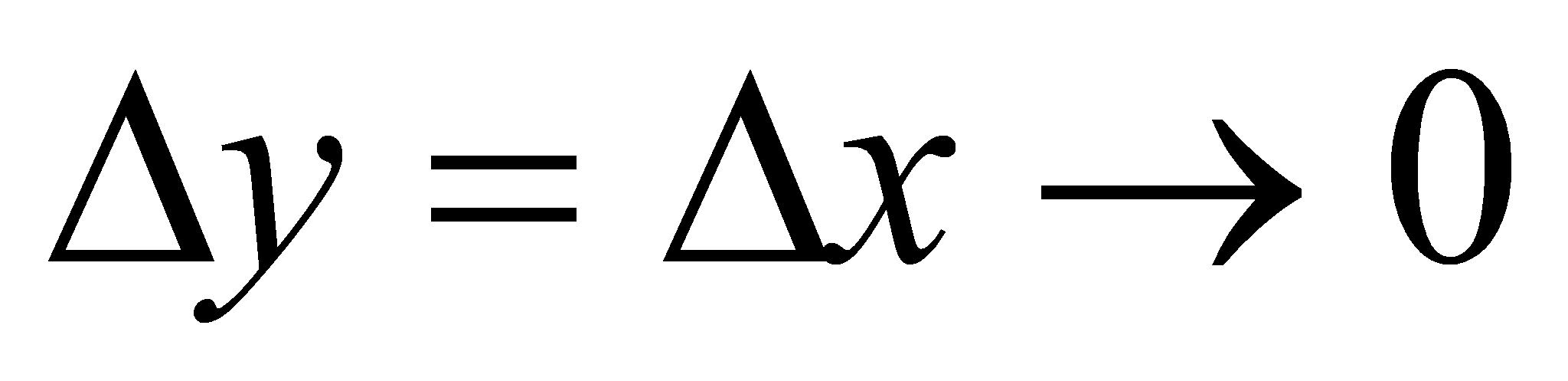 при .

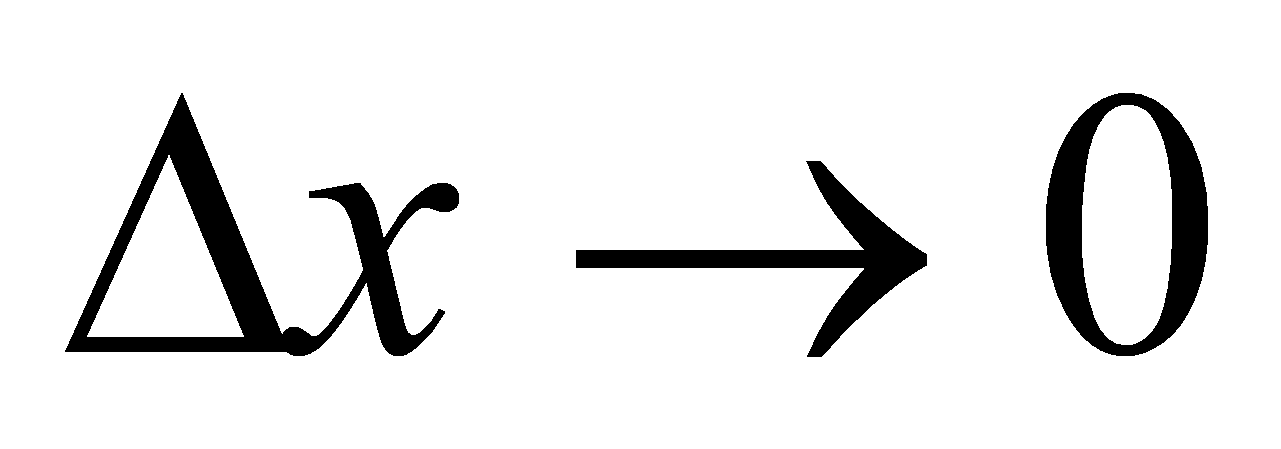3. f(x) = 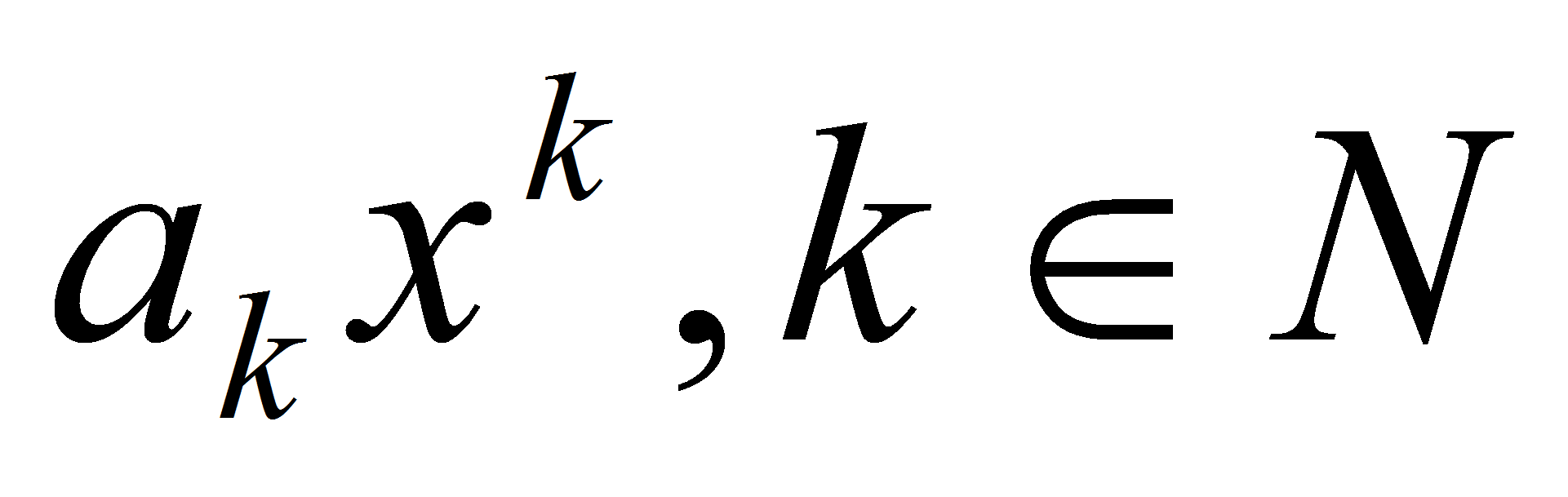, непрерывна на R как произведение непрерывных функций.

4. f(x) = 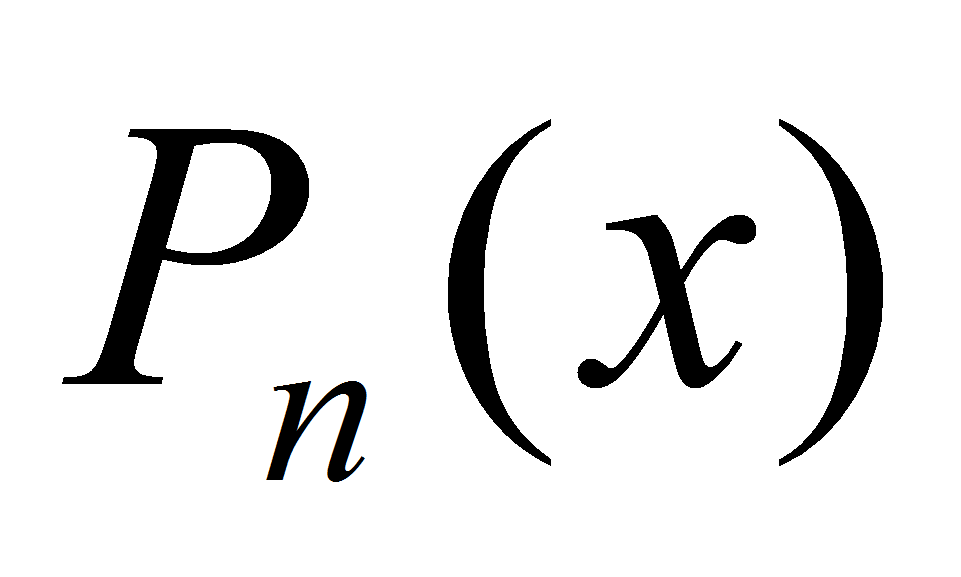, непрерывна на R, т.к. многочлен  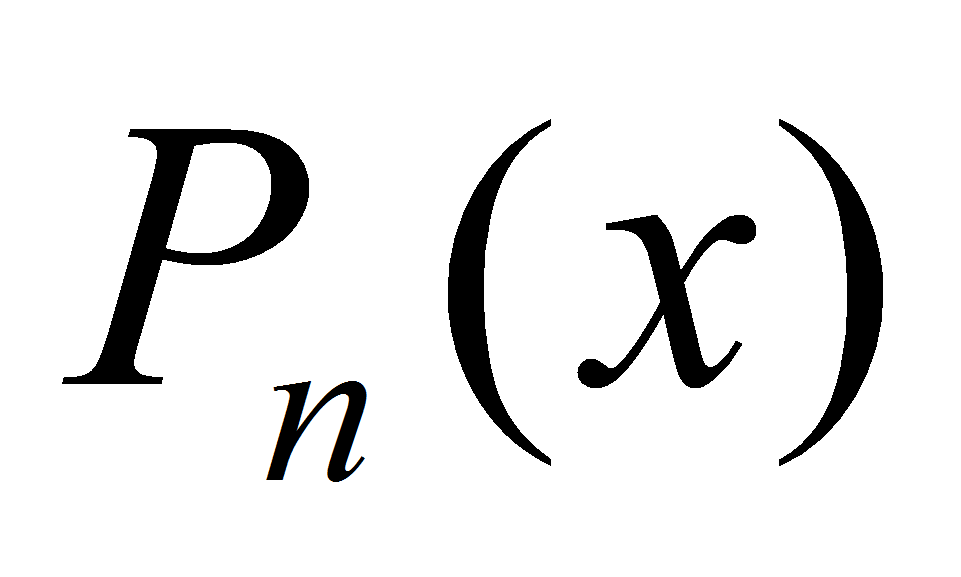есть сумма непрерывных функций.

5. f(x) = 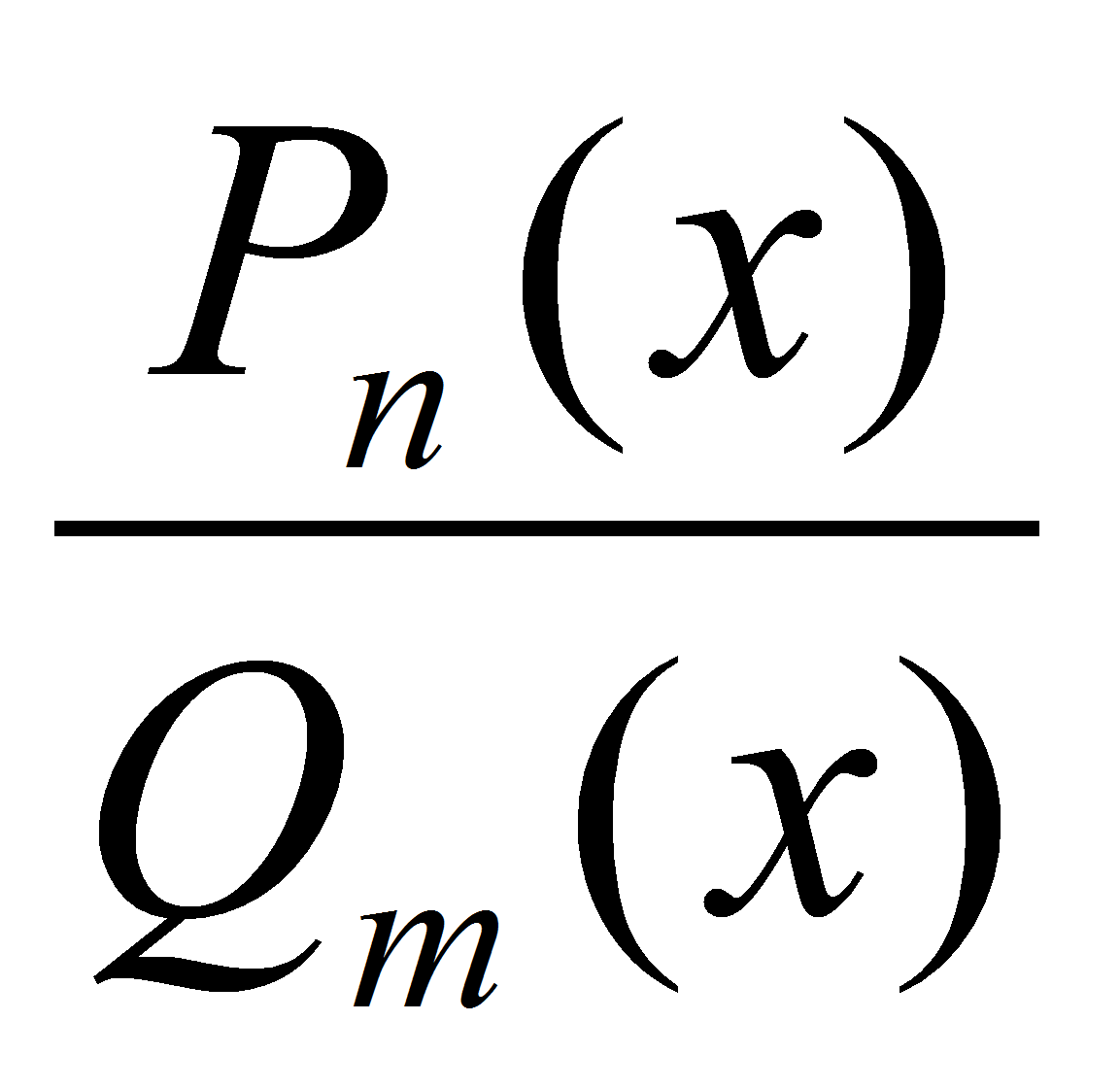, где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций.

6. f(x) = sin(x), f(x) = cos(x)

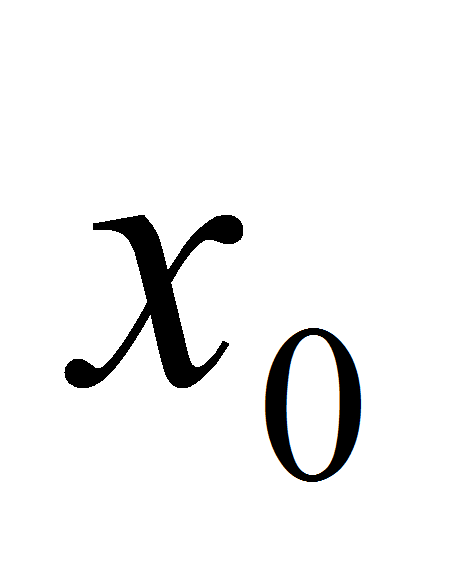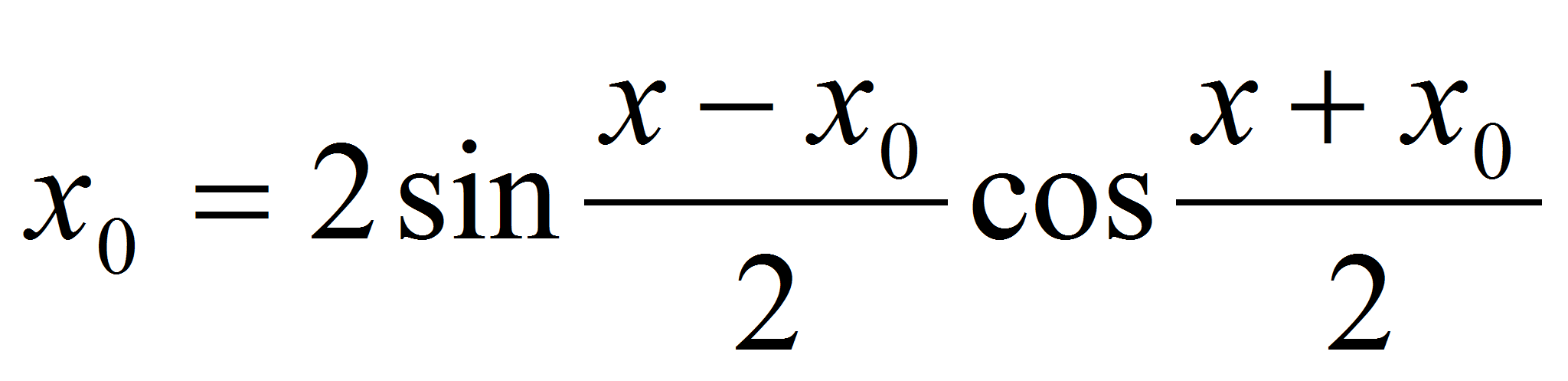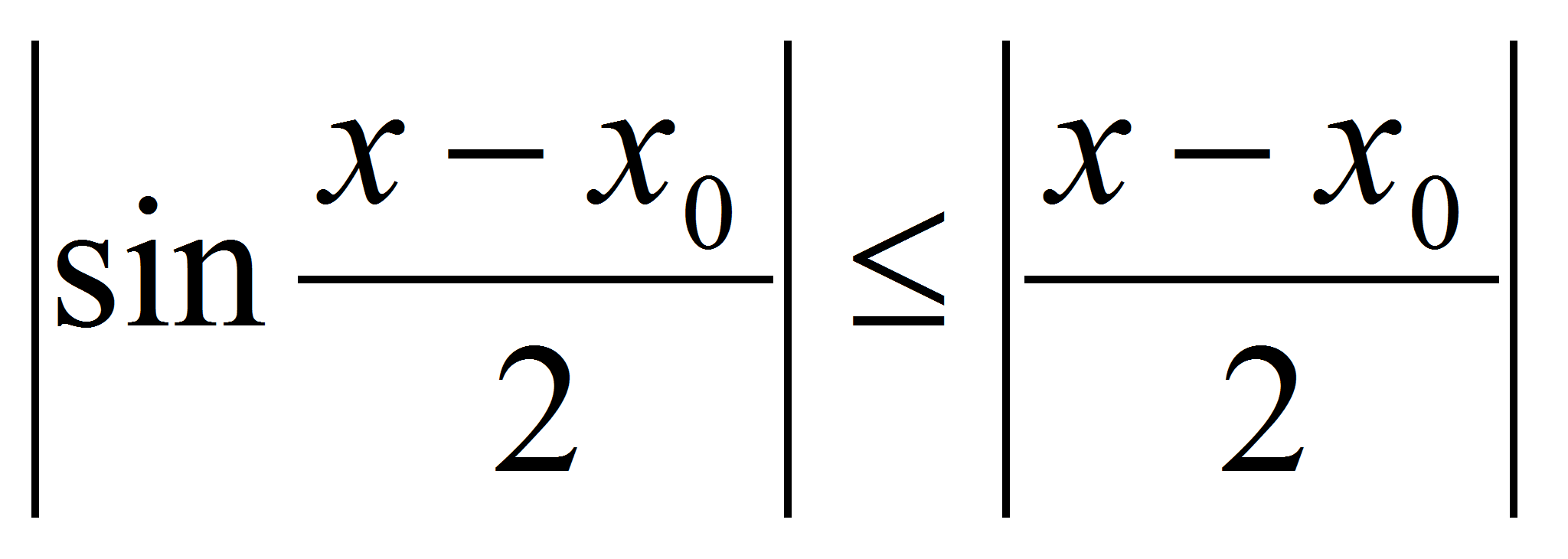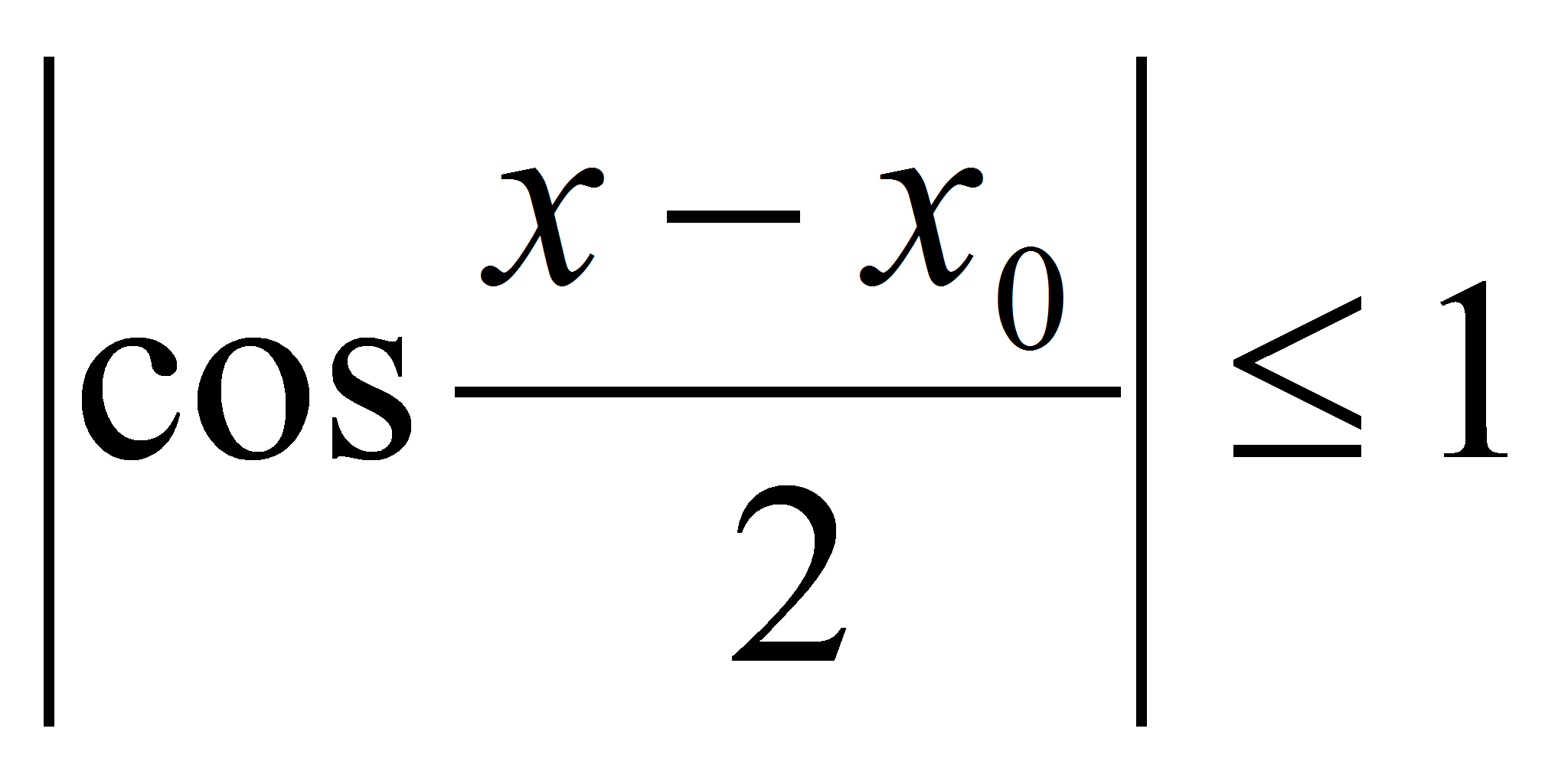Пусть  – произвольная точка множества R. Тогда sinx-sin. Так как , а , то 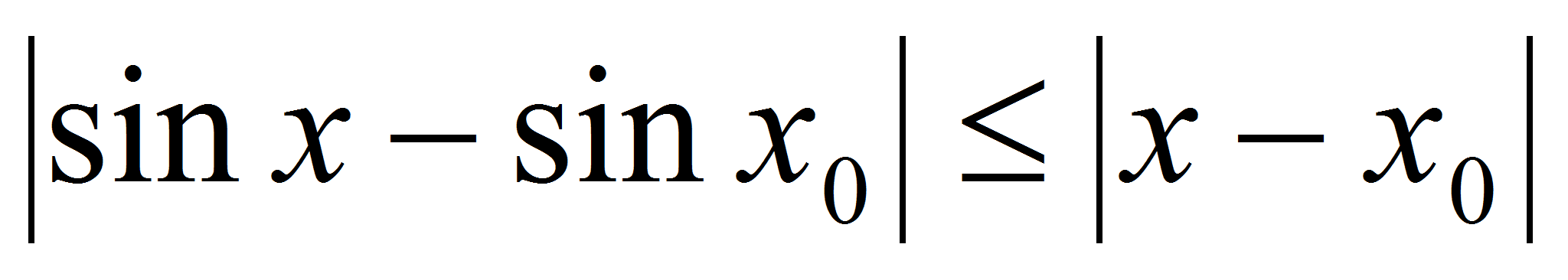 , откуда следует, что функция f(x) = sin(x) – непрерывна.

Аналогично рассуждая, можно доказать непрерывность косинуса. Из непрерывностей синуса и косинуса следуют непрерывности тангенса и котангенса, учитывая что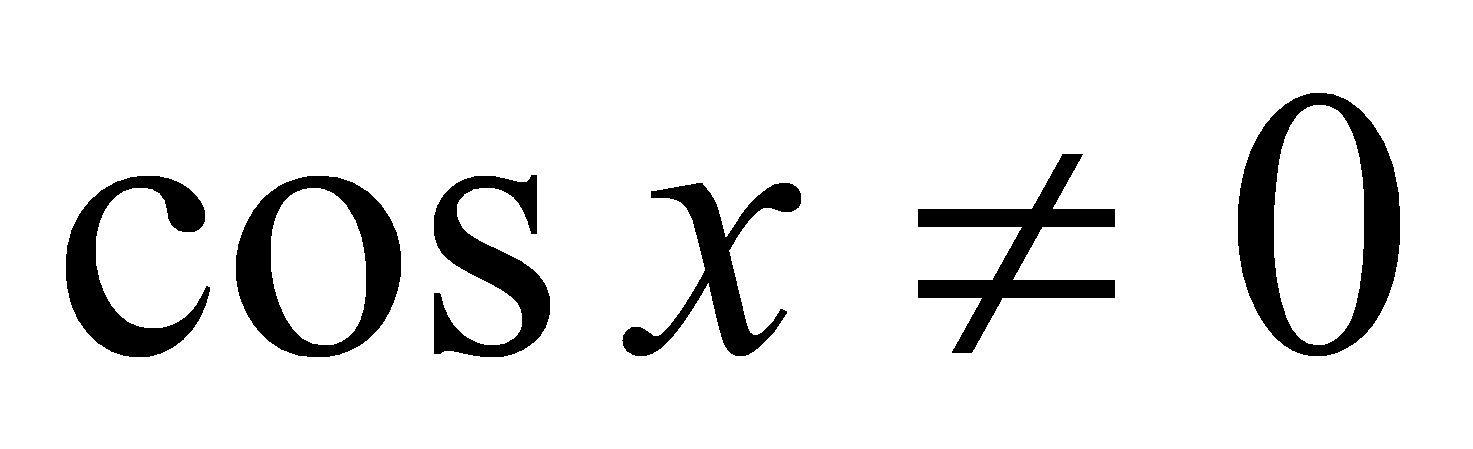(для тангенса) и 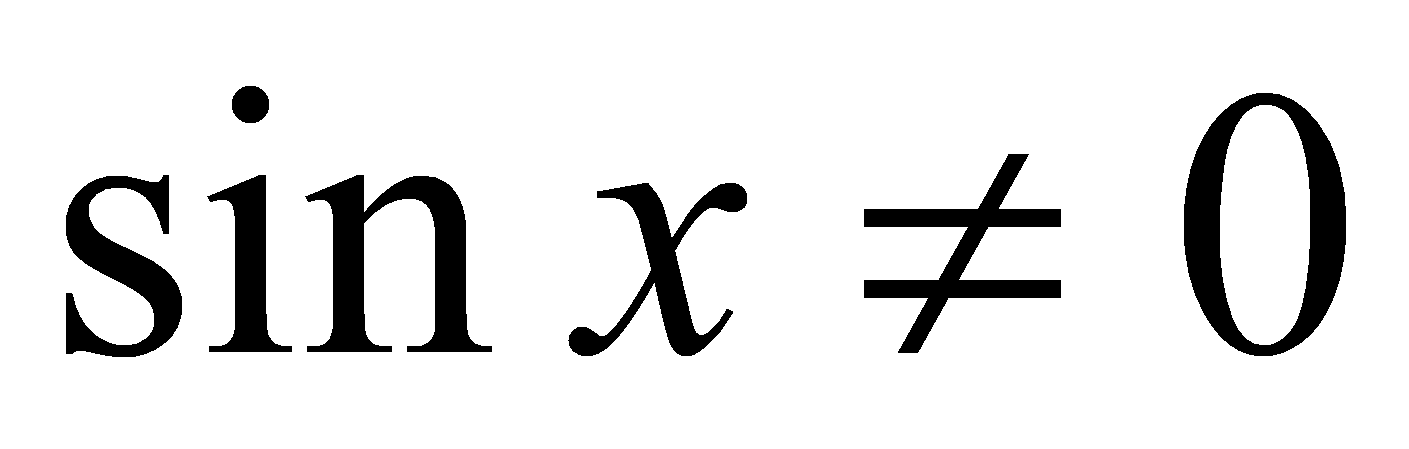(для котангенса).

7. f(x) = arcsin(x), f(x) = arccos(x), f(x) = arctg(x), f(x) = arcctg(x) , непрерывны на своей области определения. Это следует из теоремы об обратной функции, примененной не ко всей тригонометрической функции (к примеру, sin(x)), а к ее отрезку (для sin(x) это отрезок ).

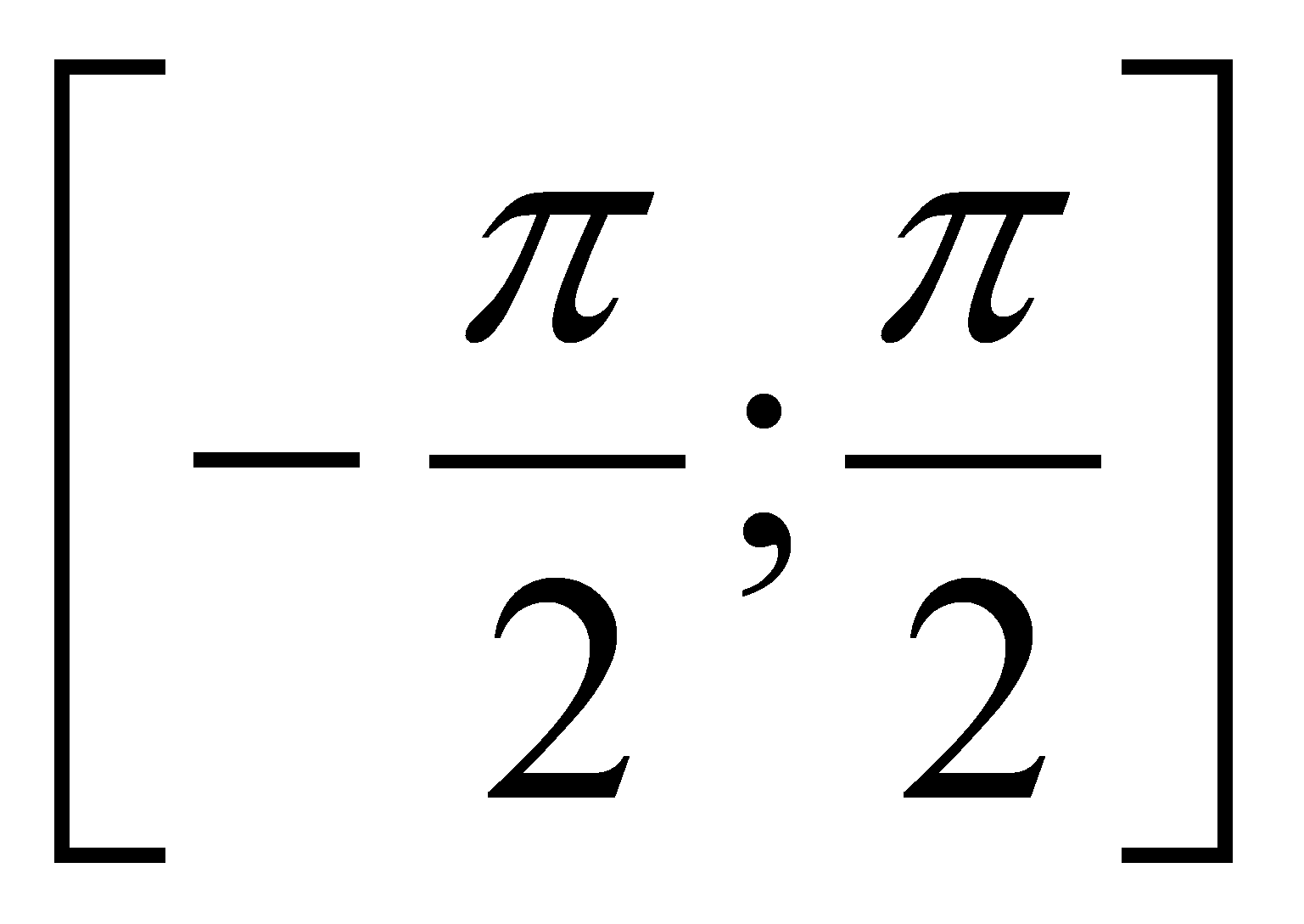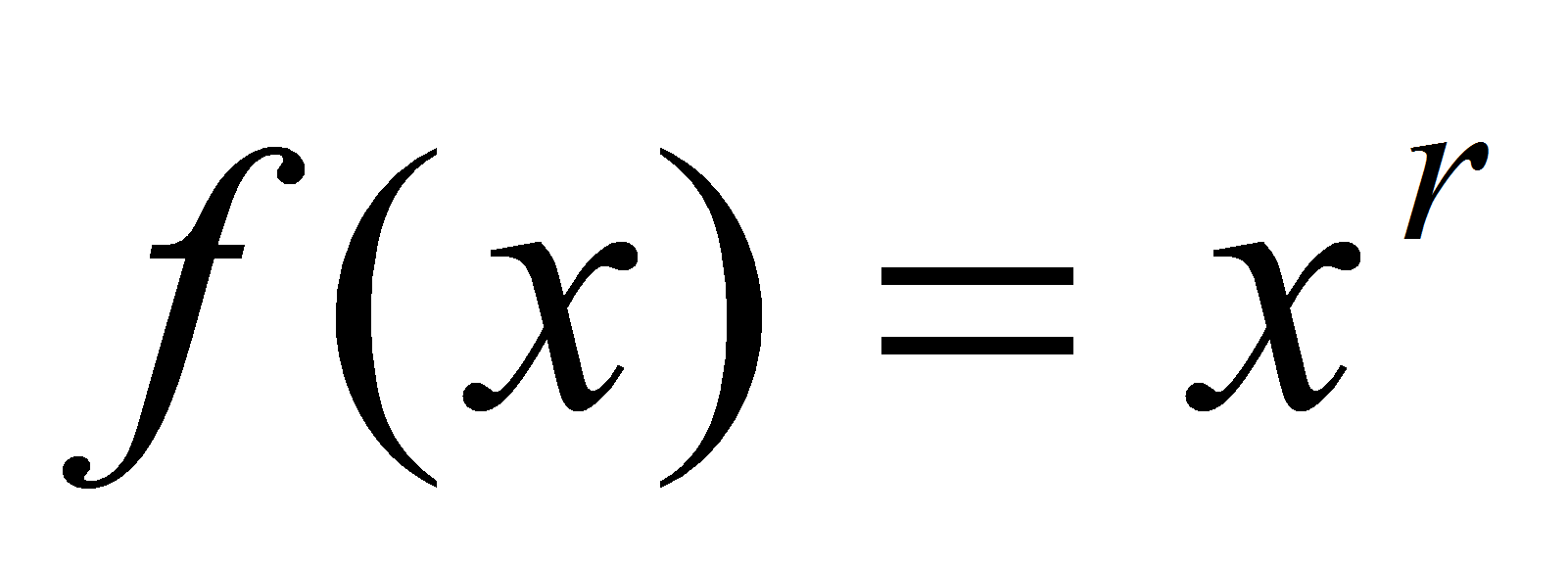8. , где r – рациональное. Представим r = m / n, 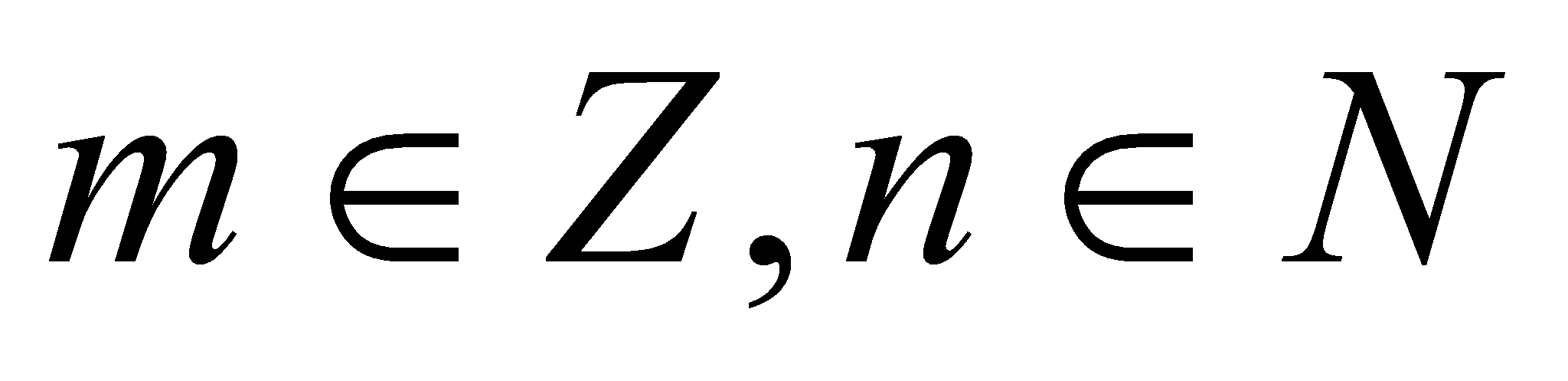. Тогда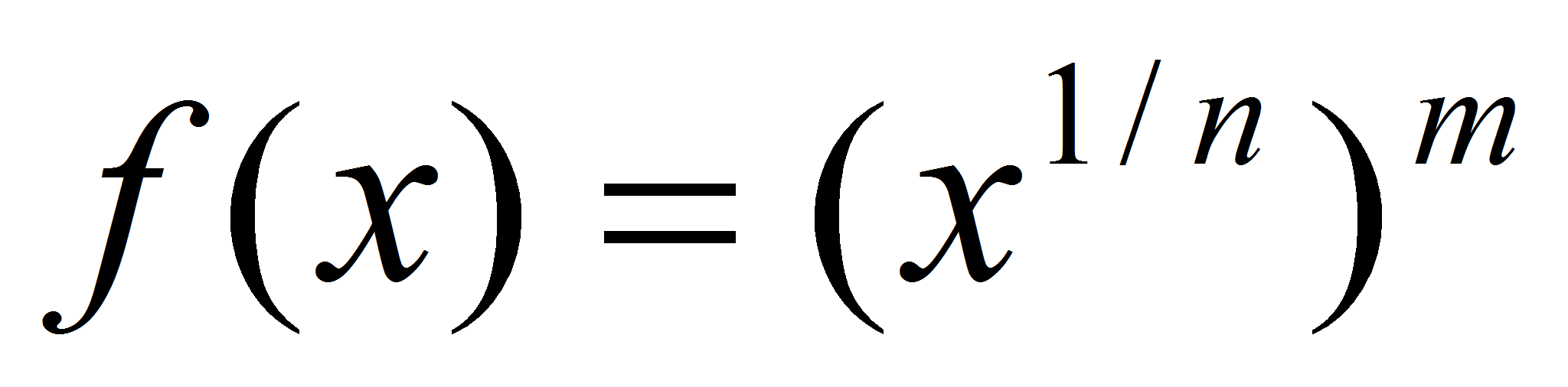. Функция  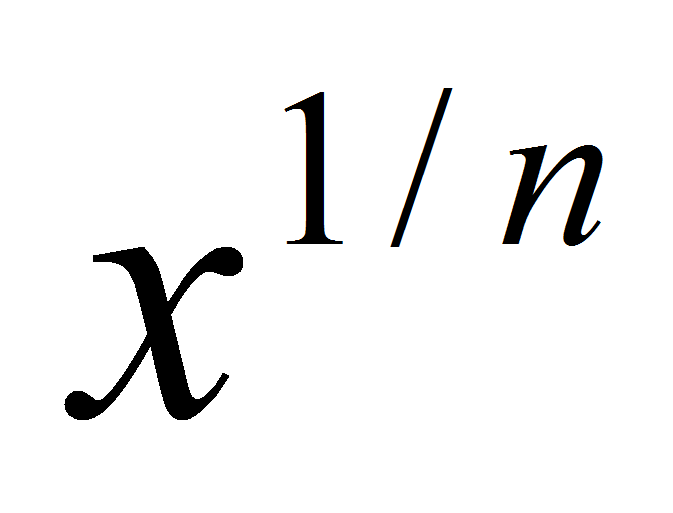непрерывна и строго возрастает на R. По п. 2 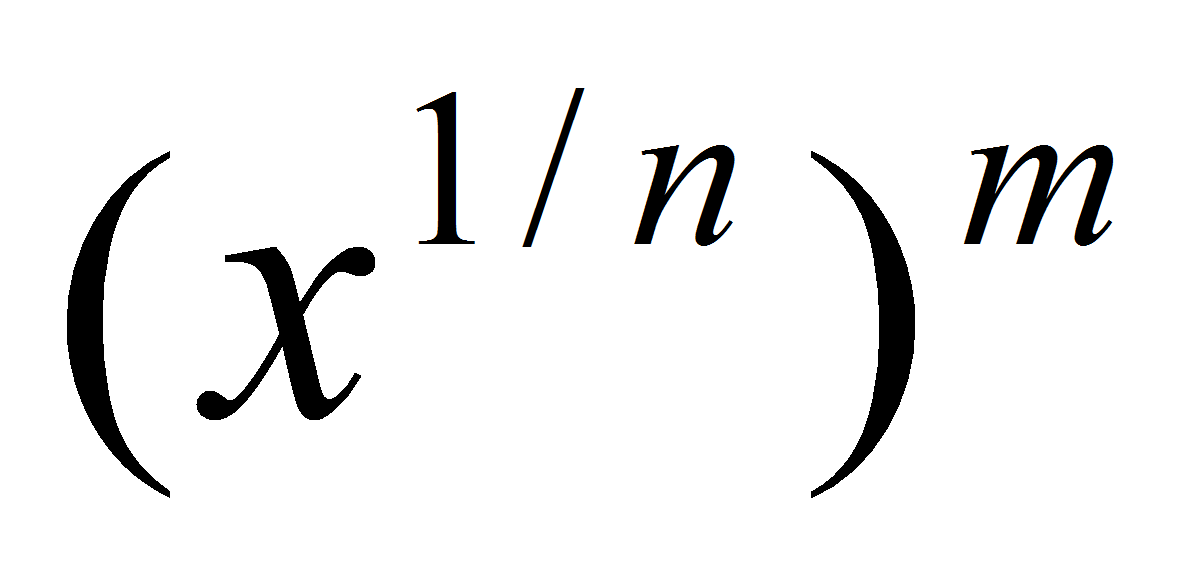также непрерывна.

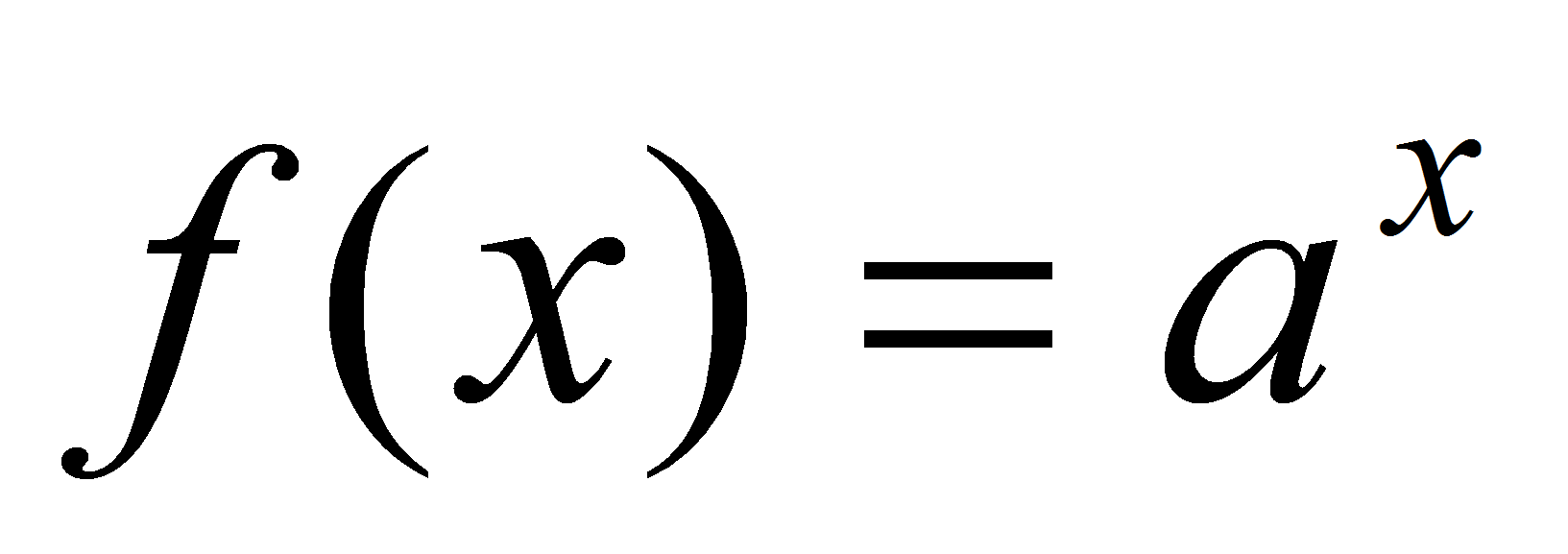9. , a > 1, непрерывна на R. Пусть  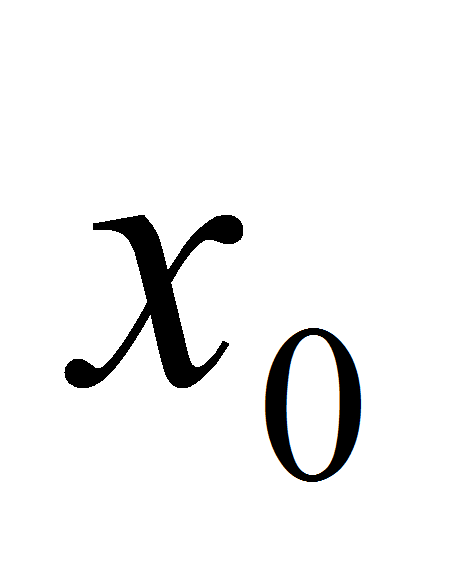– произвольная точка множества R,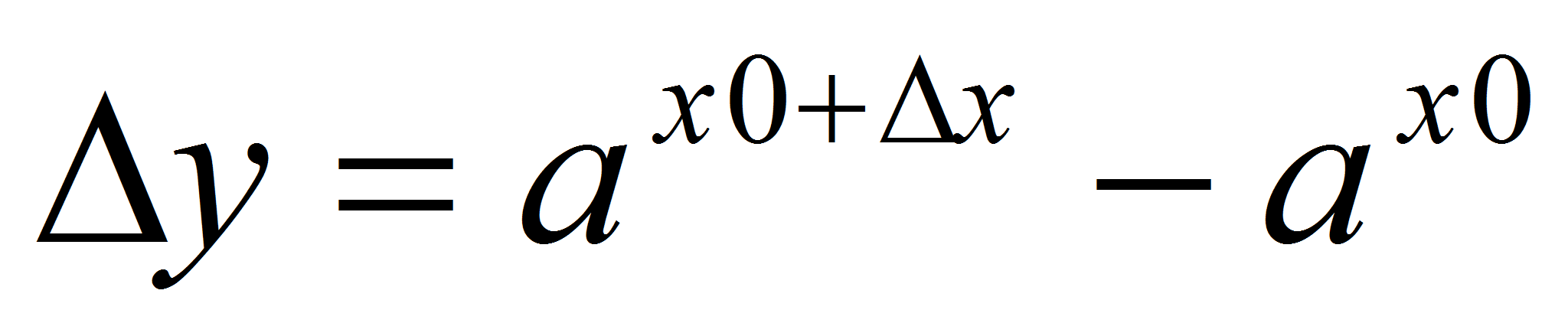=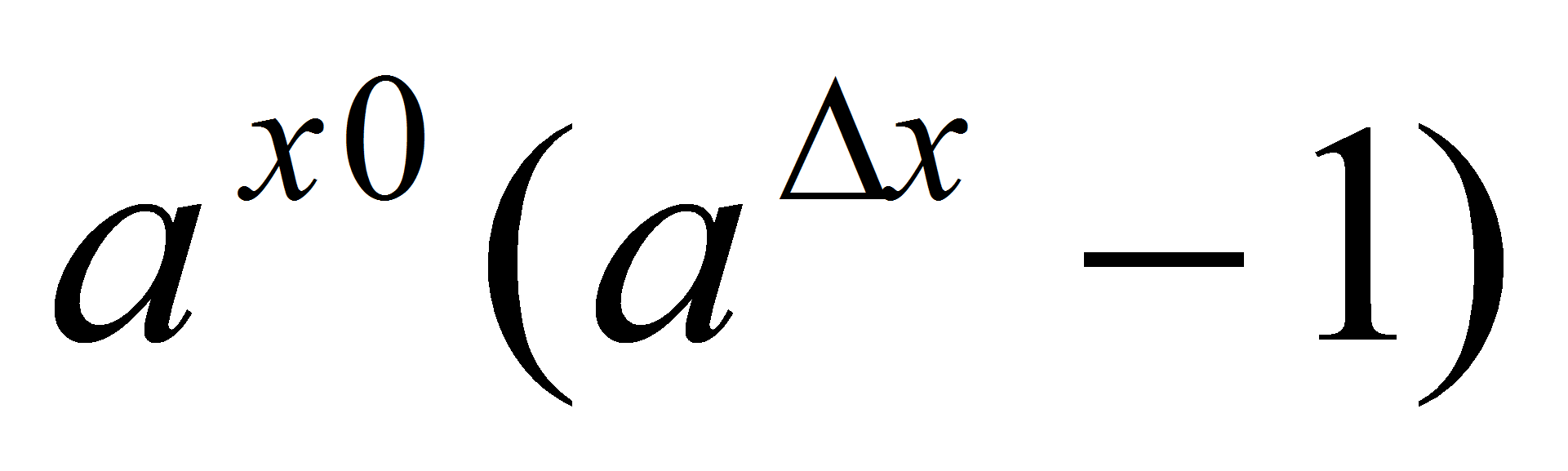. Докажем, что 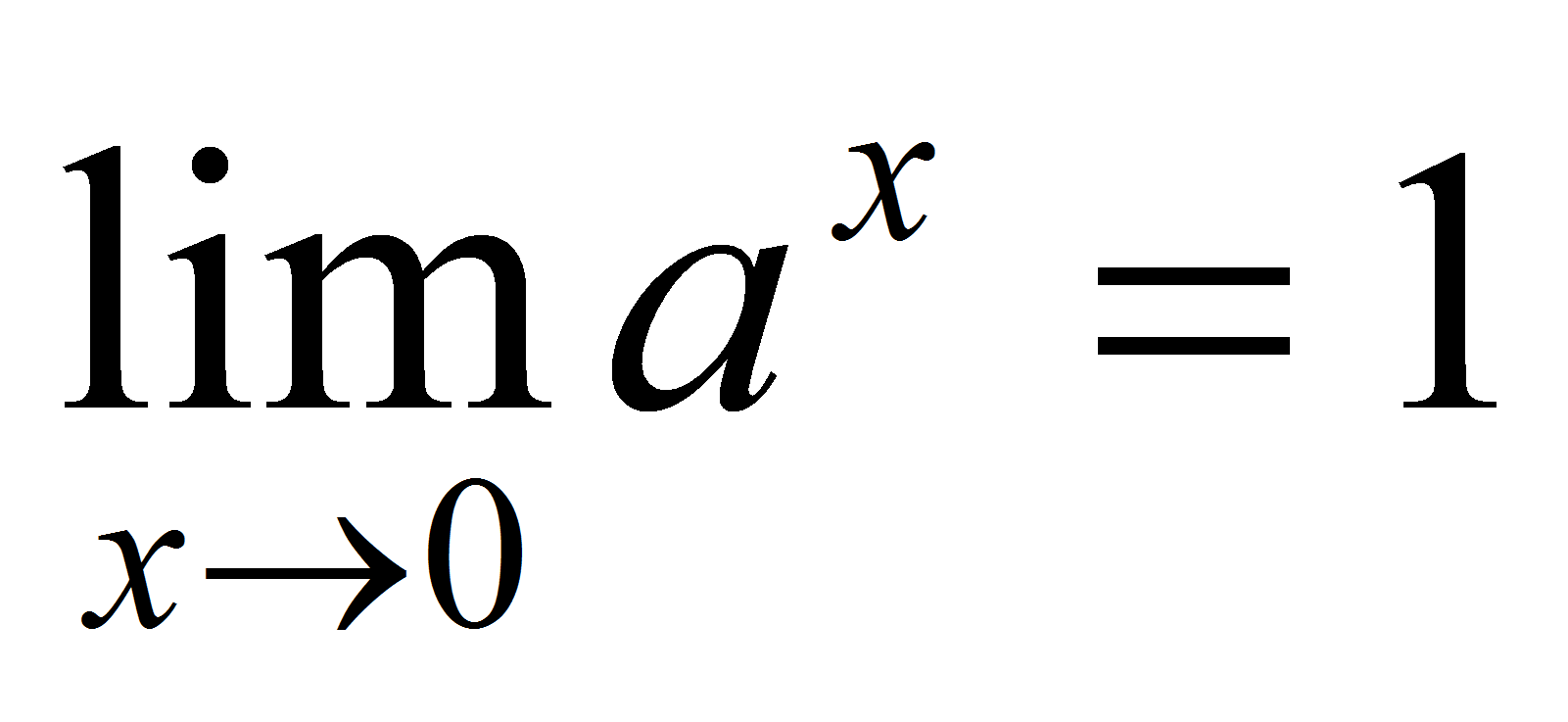. Пусть  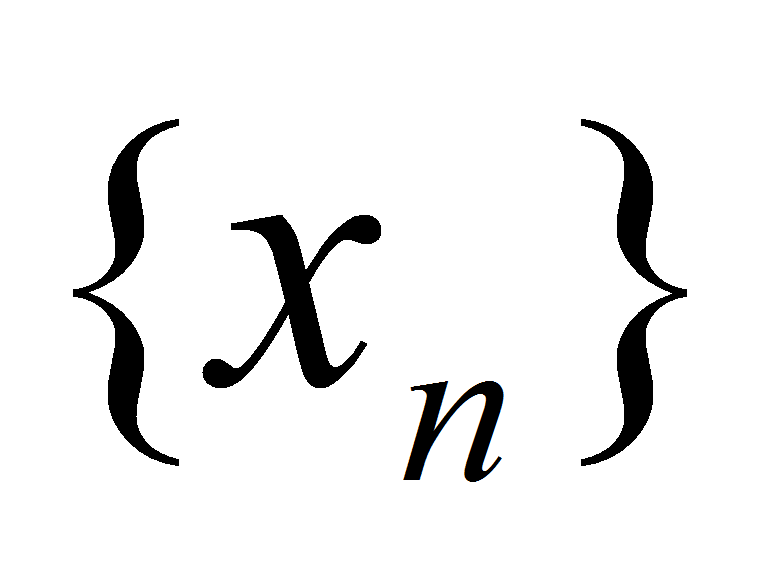- произвольная последовательность вещественных чисел такая, что 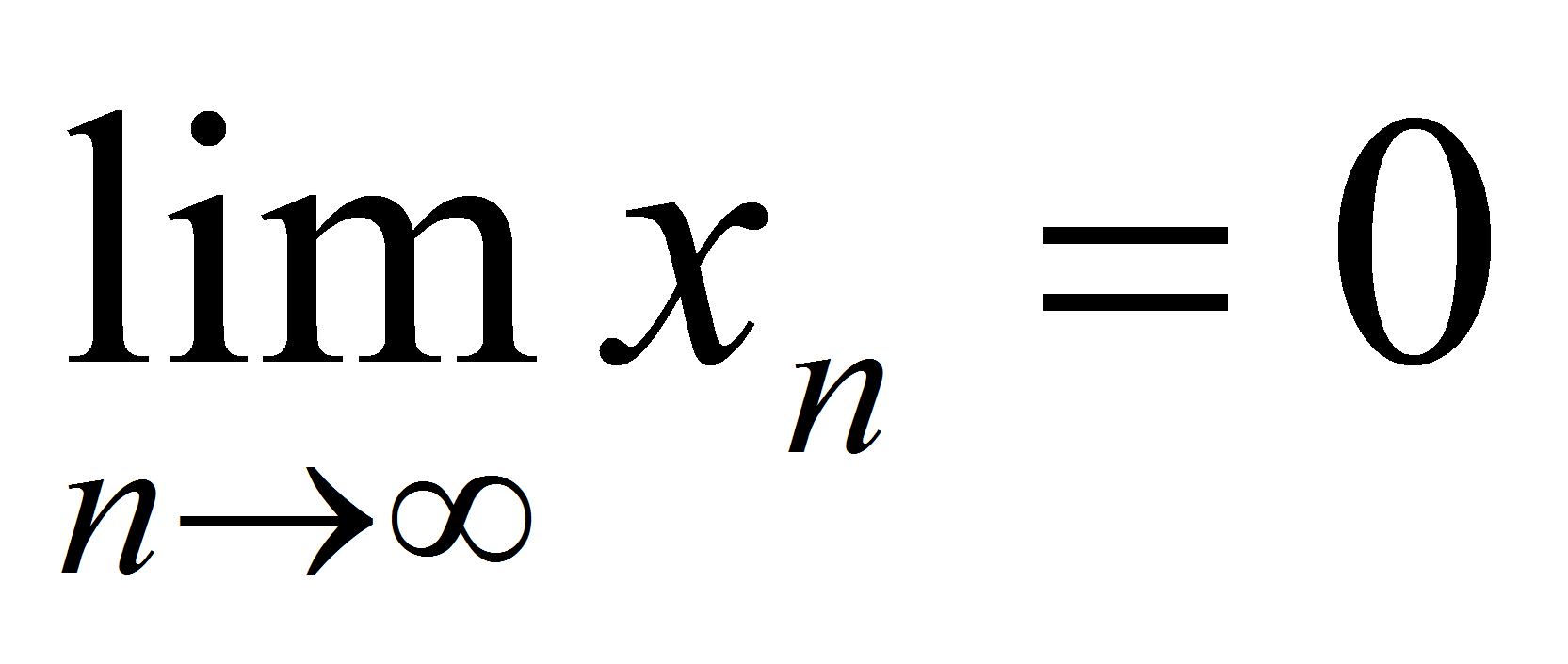. В силу свойств вещественных чисел найдутся последовательности рациональных чисел 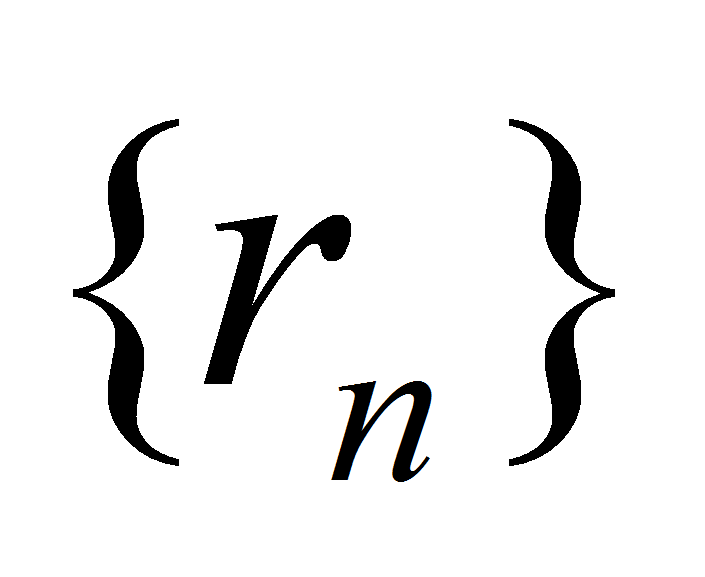и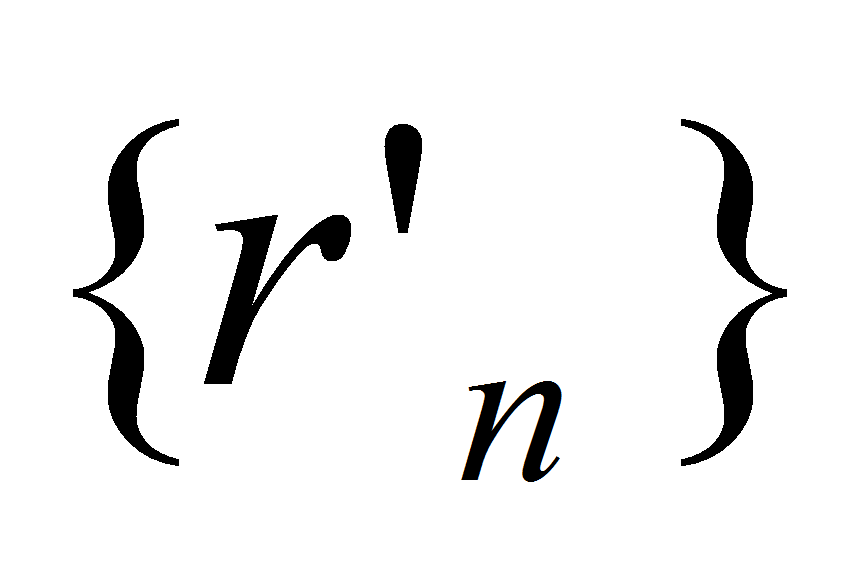, удовлетворяющие при 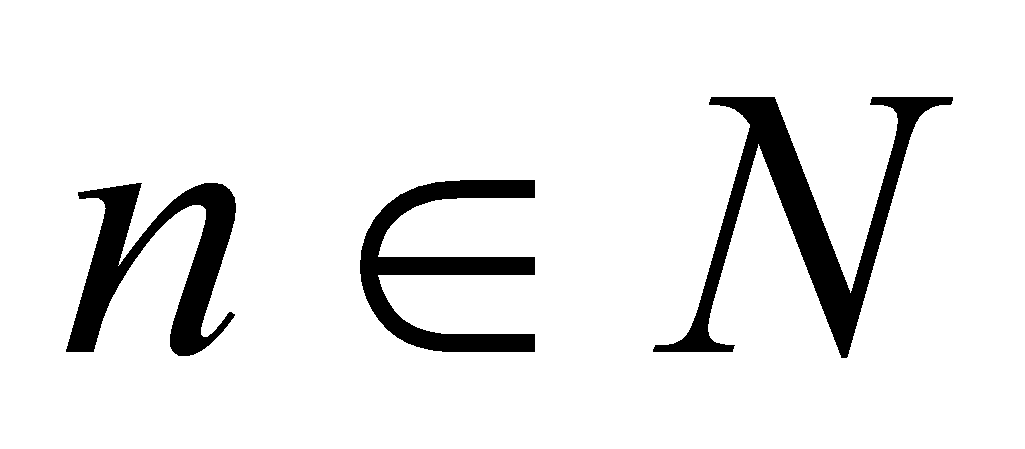условию: 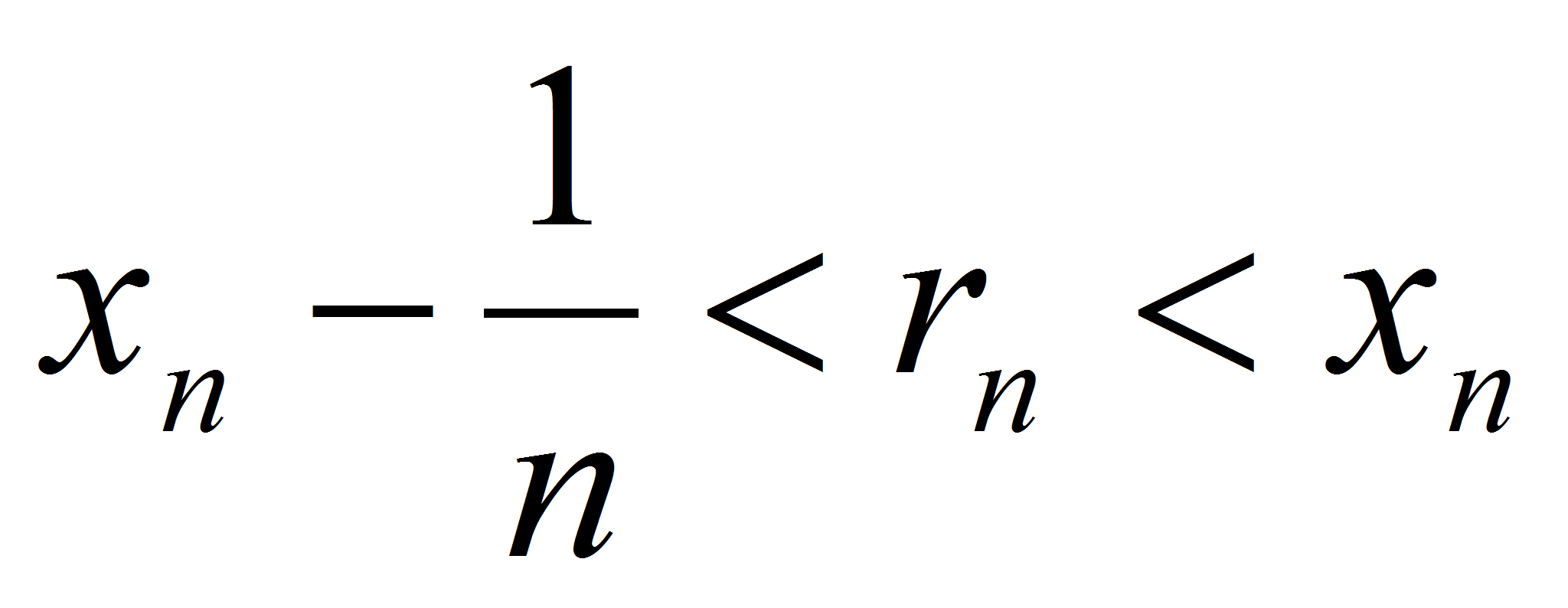<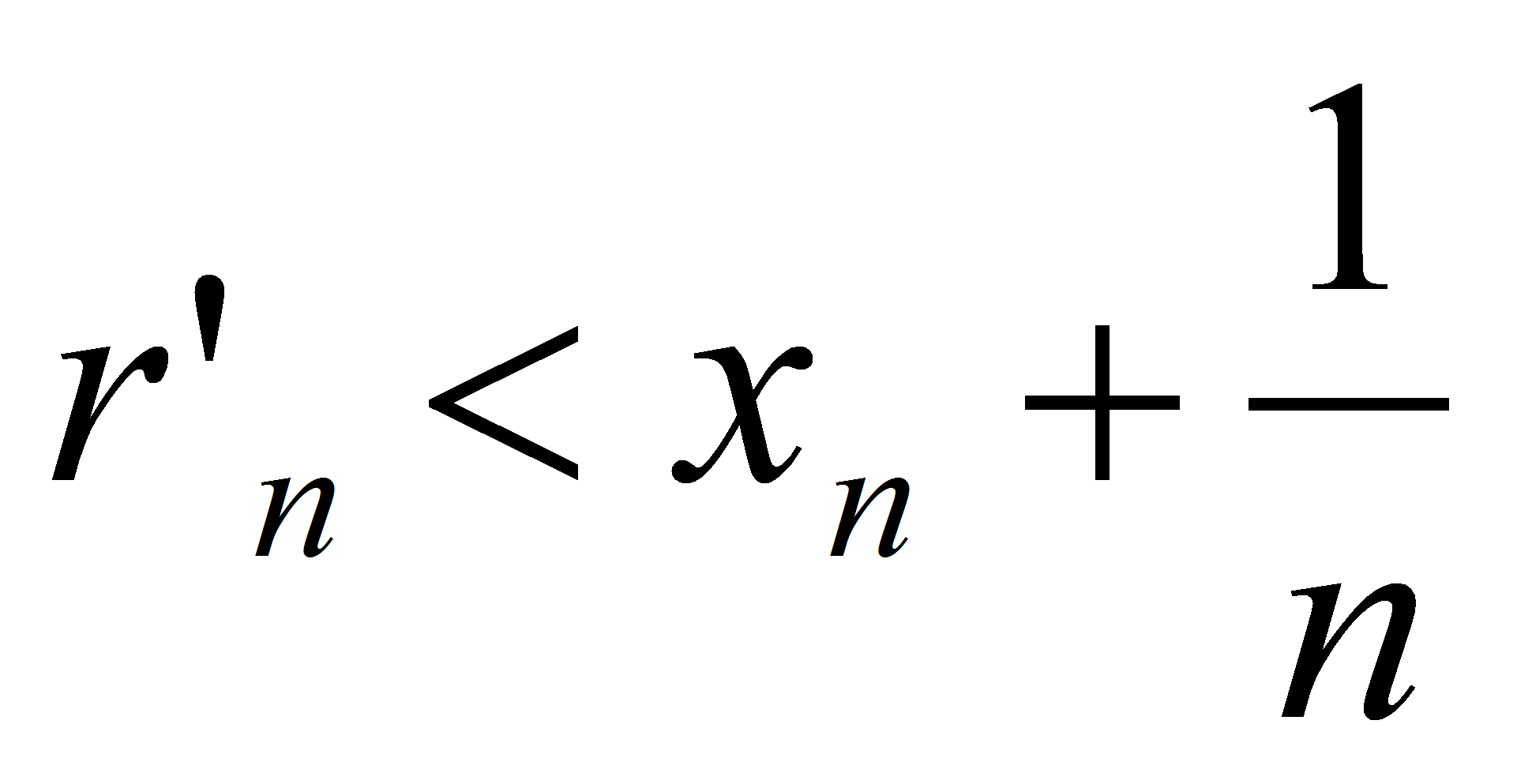, откуда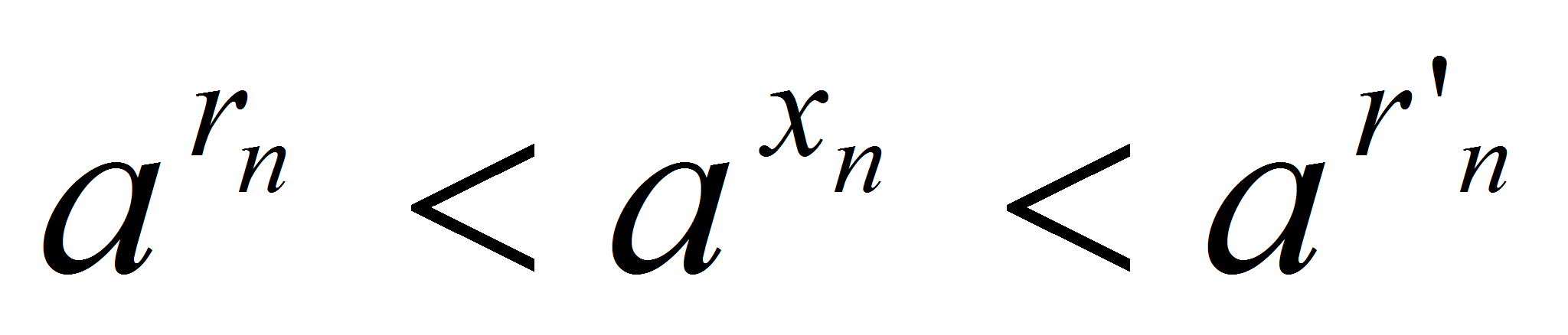. Так как  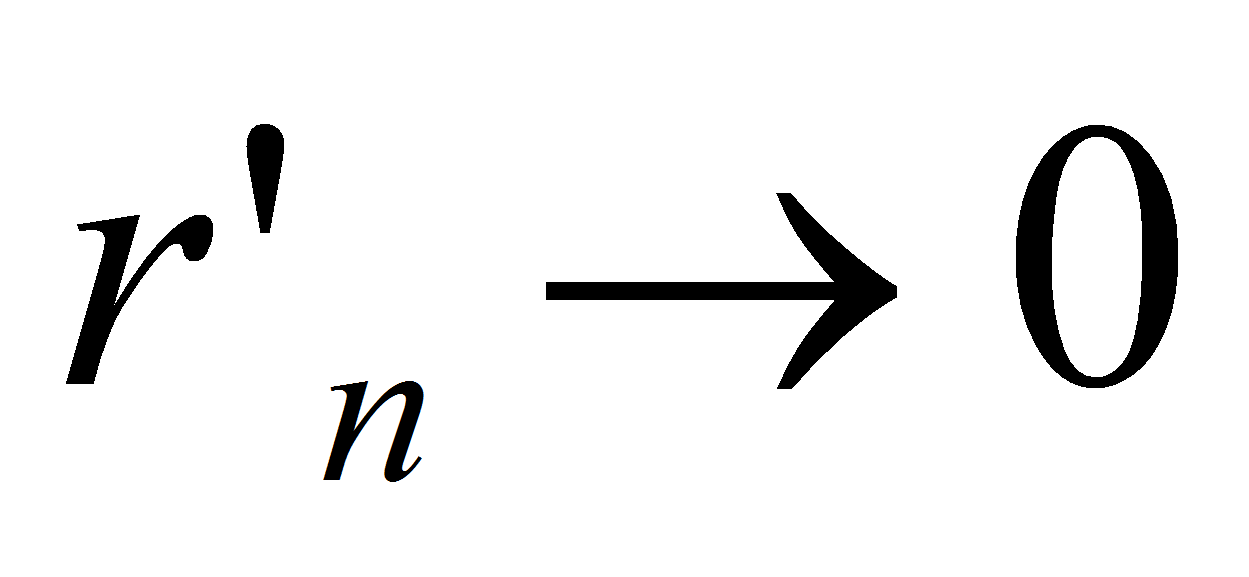и , то 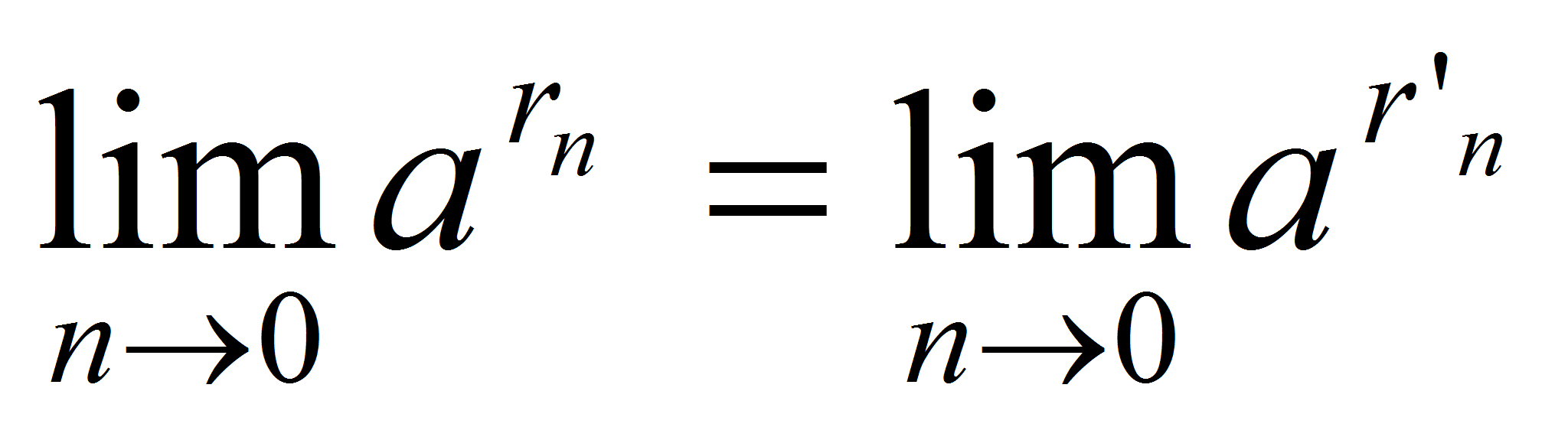=1. Отсюда и 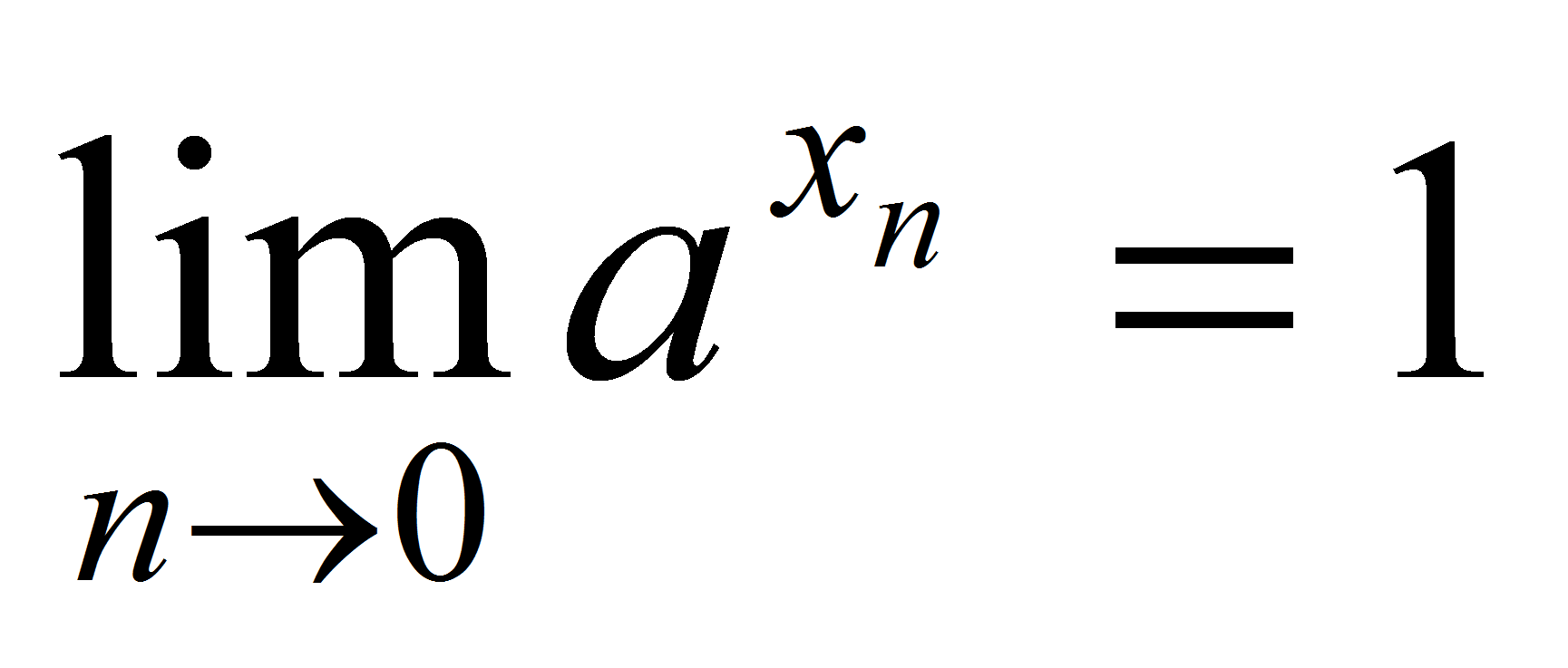, ч.т.д.

10. Логарифмическая функция непрерывна, что следует из непрерывности показательной функции по теореме об обратной функции.