Функция 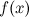 называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
- функция
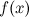 определена в точке
определена в точке  и ее окрестности;
и ее окрестности; - существует конечный предел функции
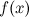 в точке
в точке  ;
; - это предел равен значению функции в точке
 , т.е.
, т.е. 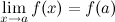
 |
|
||||||
Вопрос 30. Непрерывность функции в точке. Арифм. операции.
Понятие непрерывности функции в точкеОсновные понятия и определенияОпределение
Функция
Замечание
При нахождении предела функции
Пусть даны две функции ►Теорема 24.Сумма двух функций, непрерывных в данной точке, непрерывна в этой же точке. ►Теорема 25.Произведение двух функций, непрерывных в данной точке, непрерывно в этой же точке. ►Теорема 26.Частное двух функций, непрерывных в данной точке, непрерывно в данной точке, если значение знаменателя в данной точке не равно нулю. Доказательство этих теорем следует из Определение 71 и соответствующих теорем о пределе суммы, произведения и частного в данной точке. Пример 79.Докажите, что любая целая рациональная функция (многочлен) Доказательство:из Пример 78 следует, что функция Пример 80.Докажите, что рациональная функция Доказательство:из Пример 79 следует, что Рассмотрим композицию непрерывных функций. ►Теорема 27.Пусть функция Доказательство:зададим Это и значит, что функция Замечание. ►Теорема 27 обобщается на любое количество композиций непрерывных функций. Пример 81.Докажите, что функция Доказательство:пусть
Конечно, к тому же выводу мы пришли бы, используя Определение 73. Действительно, неравенство
|
|||||||
|
|||||||