Предел функции. Число L называется пределом функции  y = f ( x ) при  x, стремящемся к  a :
 

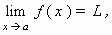
если для любого 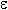  > 0 найдётся такое положительное число  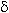=  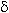(  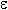), зависящее от  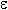, что из условия | x - a | <  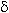следует  |  f ( x ) – L | <  .

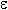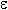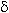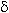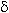Это определение означает, что L есть предел функции  y = f ( x ), если значение функции неограниченно приближается к  L , когда значение аргумента  x приближается к  a. Геометрически это значит, что для любого   > 0  можно найти такое число  , что если  x  находится в интервале ( a- , a +  ), то значение функции лежит в интервале 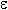( L - ,  L + 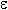 ). Отметим, что в соответствии с этим определением аргумент функции лишьприближается  к  a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.

Бесконечные пределы в конечной точке

Проколотой окрестностью точки  называется: