Вопрос 22. Натуральные логарифмы. у=ех. Гипербалические функции.

Логарифмом положительного числа N по основанию ( b > 0, b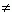1 ) называется показатель степени x , в которую нужно возвести b, чтобыполучить N .

Обозначение логарифма:

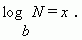
Эта запись равнозначна следующей: bx = N .

Экспонента – это показательная функция y(x) = e x, производная которой равна самой функции.

График экспоненты

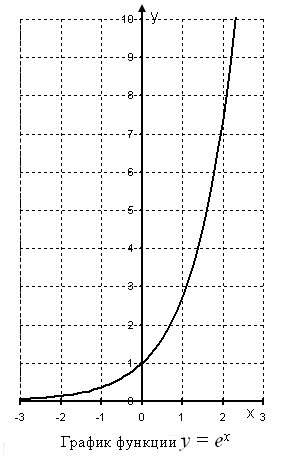График экспоненты е в степени х На графике представлена экспонента, е в степени х.
y(x) = е х
На графике видно, что экспонента монотонно возрастает.

Формулы

Основные формулы такие же, как и для показательной функции с основанием степени е > 1.

Гиперболические функции задаются следующими формулами:

гиперболический синус:

$\mathop{\mathrm{sh}}\,x=\frac{e^x-e^{-x}}{2}$ (в зарубежной литературе обозначается $\sinh x$ )

Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.

гиперболический косинус:

$\mathop{\mathrm{ch}}\,x=\frac{e^x+e^{-x}}{2}$ (в зарубежной литературе обозначается $\cosh x$ )

Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.

гиперболический тангенс:

$\mathop{\mathrm{th}}\,x=\frac{\mathop{\mathrm{sh}}\,x}{\mathop{\mathrm{ch}}\,x}$ (в зарубежной литературе обозначается $\tanh x$ ).

Существует сленговое название: «щангенс». Однако их использование не научно.

Иногда также определяются

гиперболический котангенс:

$\mathop{\mathrm{cth}}\,x=\frac{1}{\mathop{\mathrm{th}}\,x}$ ,

гиперболические секанс и косеканс:

$\mathop{\mathrm{sch}}\,x=\frac{1}{\mathop{\mathrm{ch}}\,x}$ ,

$\mathop{\mathrm{csch}}\,x=\frac{1}{\mathop{\mathrm{sh}}\,x}$ .