Бесконечно большие.
Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение 
, что каждое следующее за ним x будет по абсолютной величине больше 
. Пишут: 
Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно.
Теорема о связи между бесконечно большой и бесконечно малой функциями:
Если функция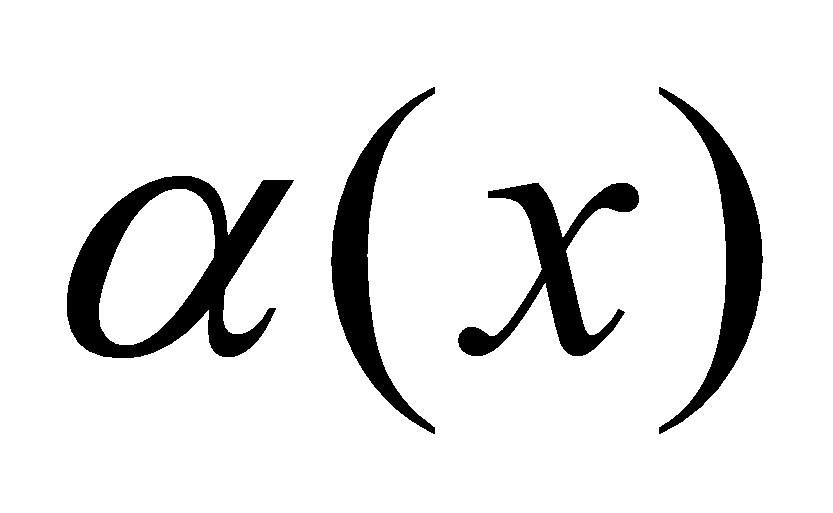 
- функция бесконечно малая (
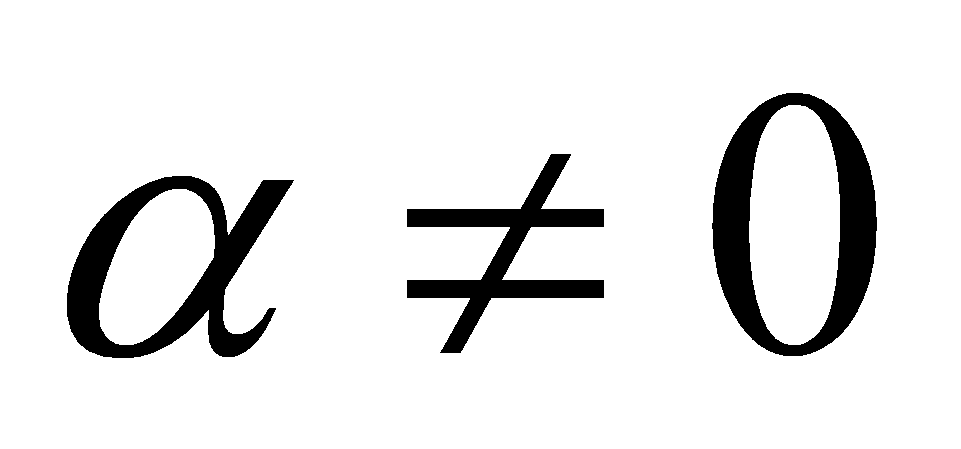), то функция 
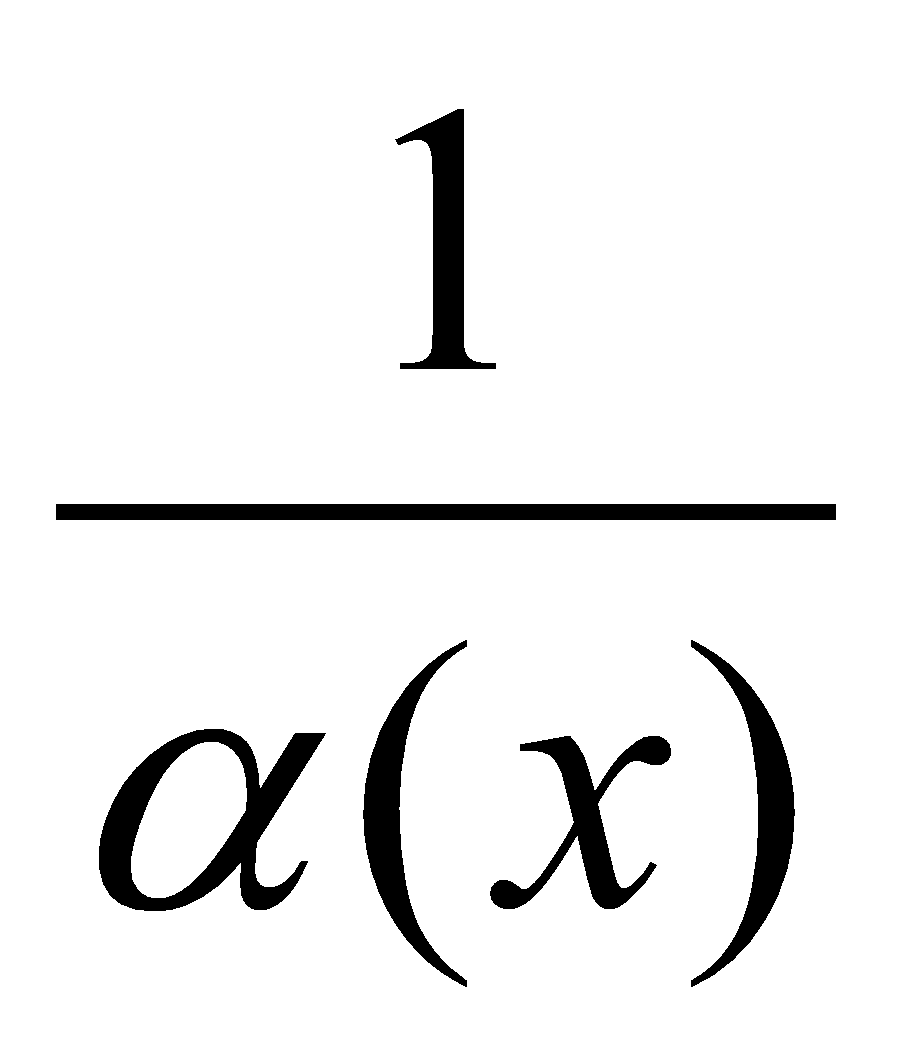есть бесконечно большая функция и наоборот.
Доказательство:
Пусть 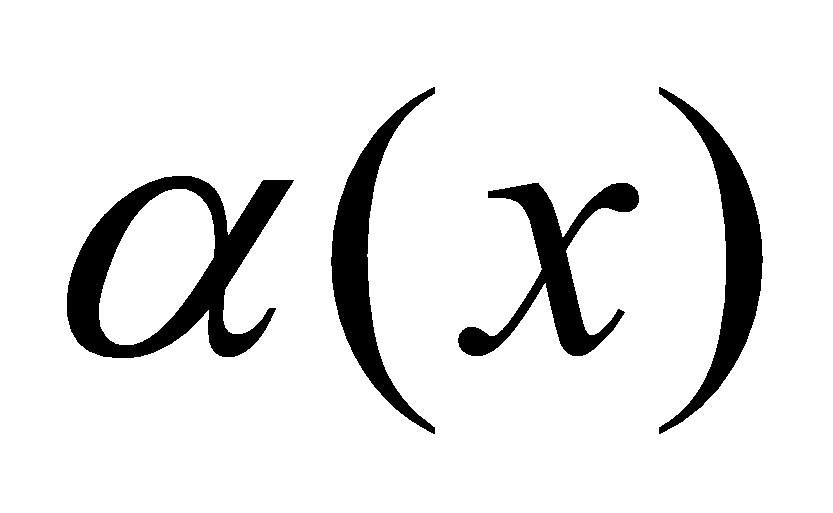- бесконечно малая функция при 
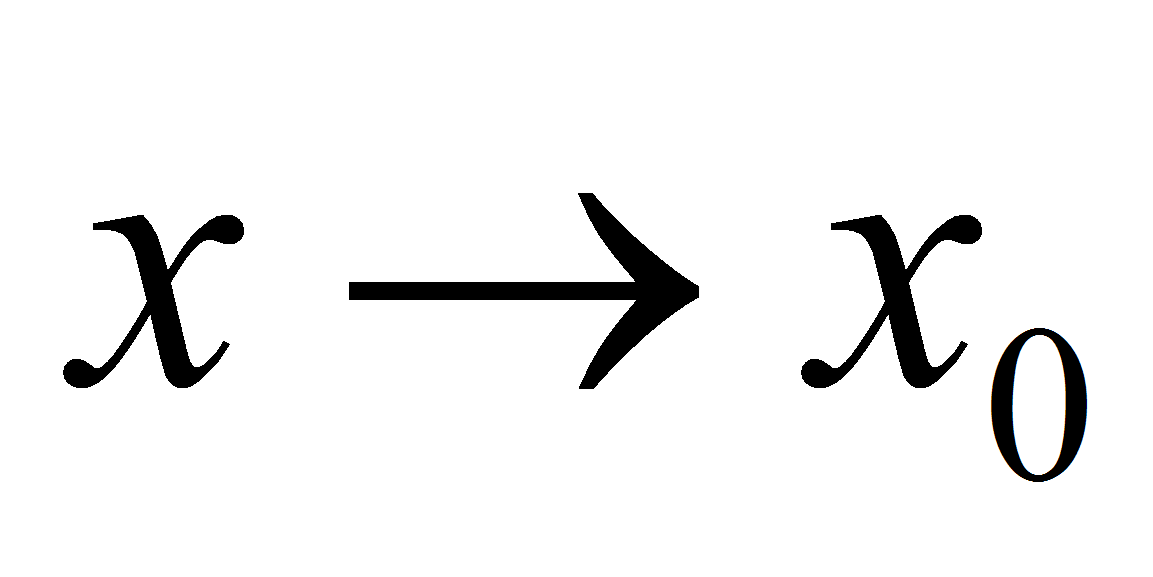, т.е. 
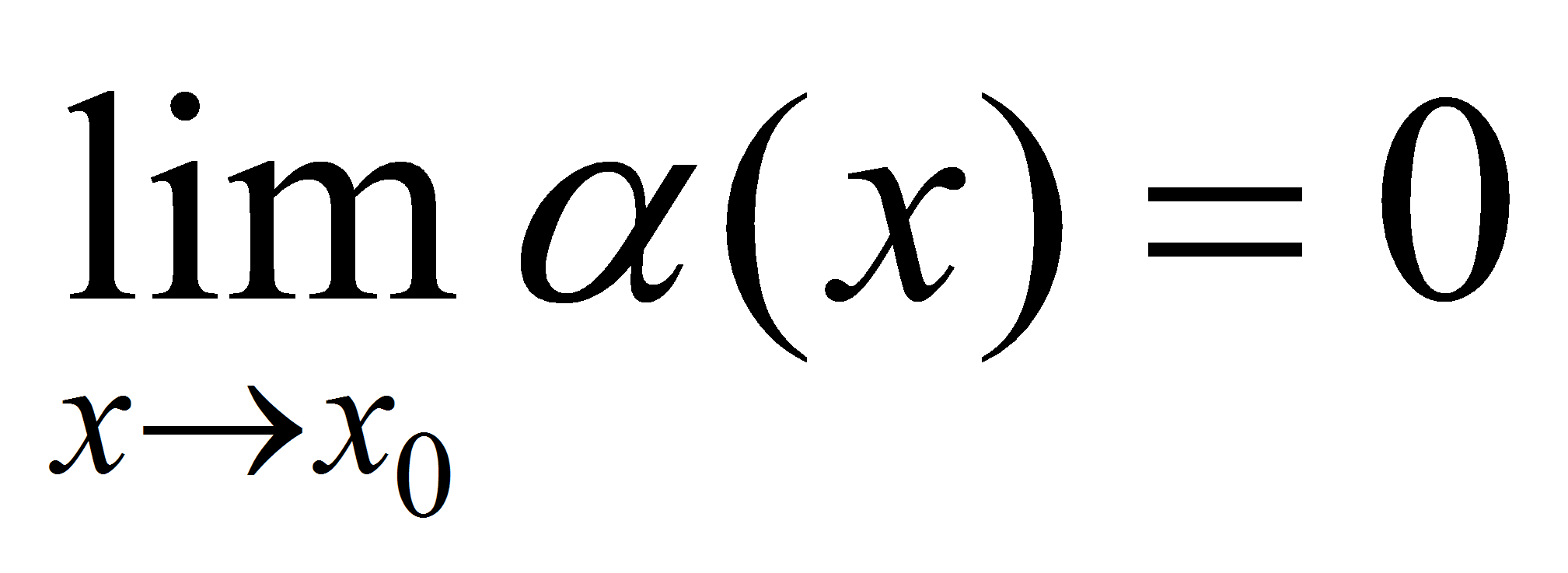. Тогда для любого числа 
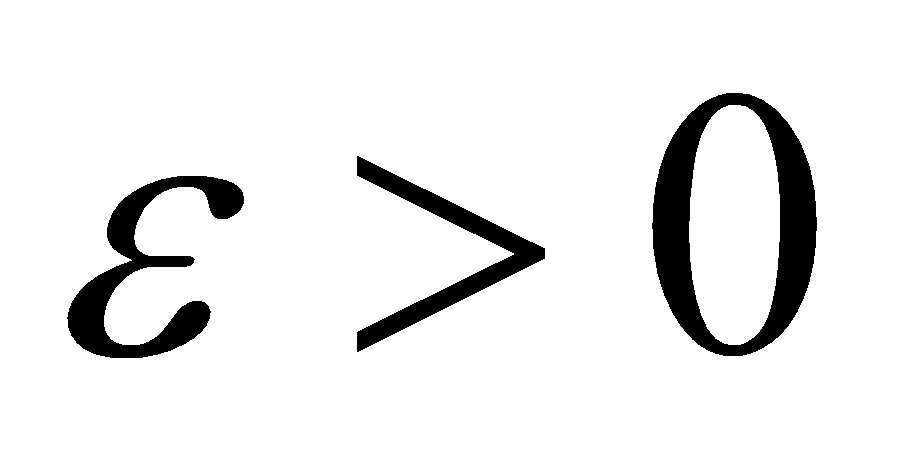существует такое число 
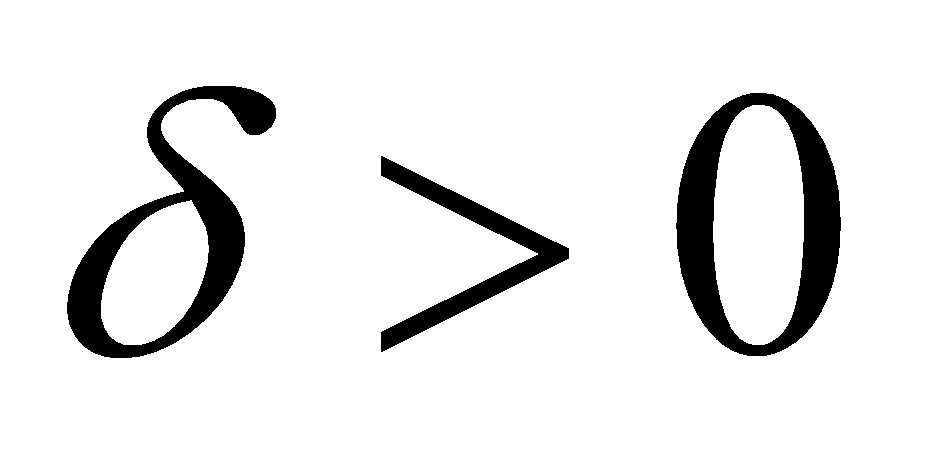, что для всех 
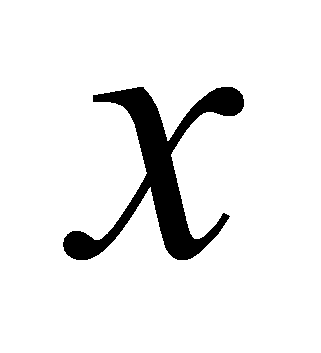, удовлетворяющих неравенству 
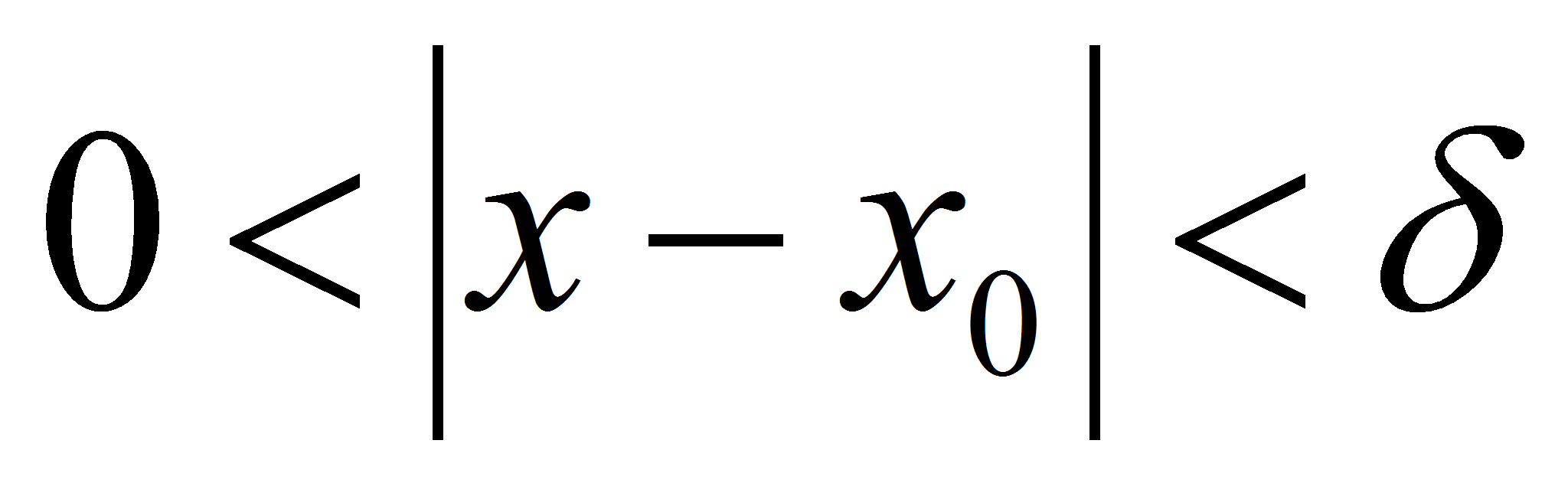, выполняется неравенство 
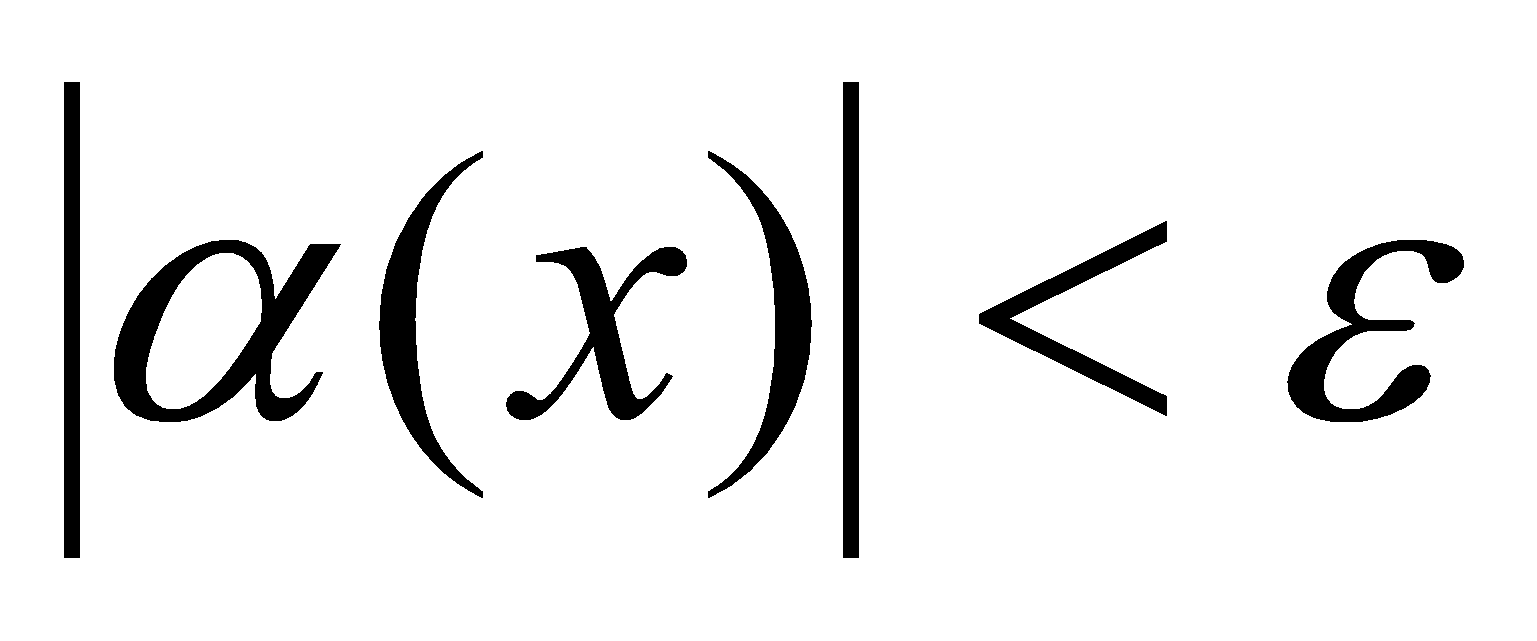, т.е. 
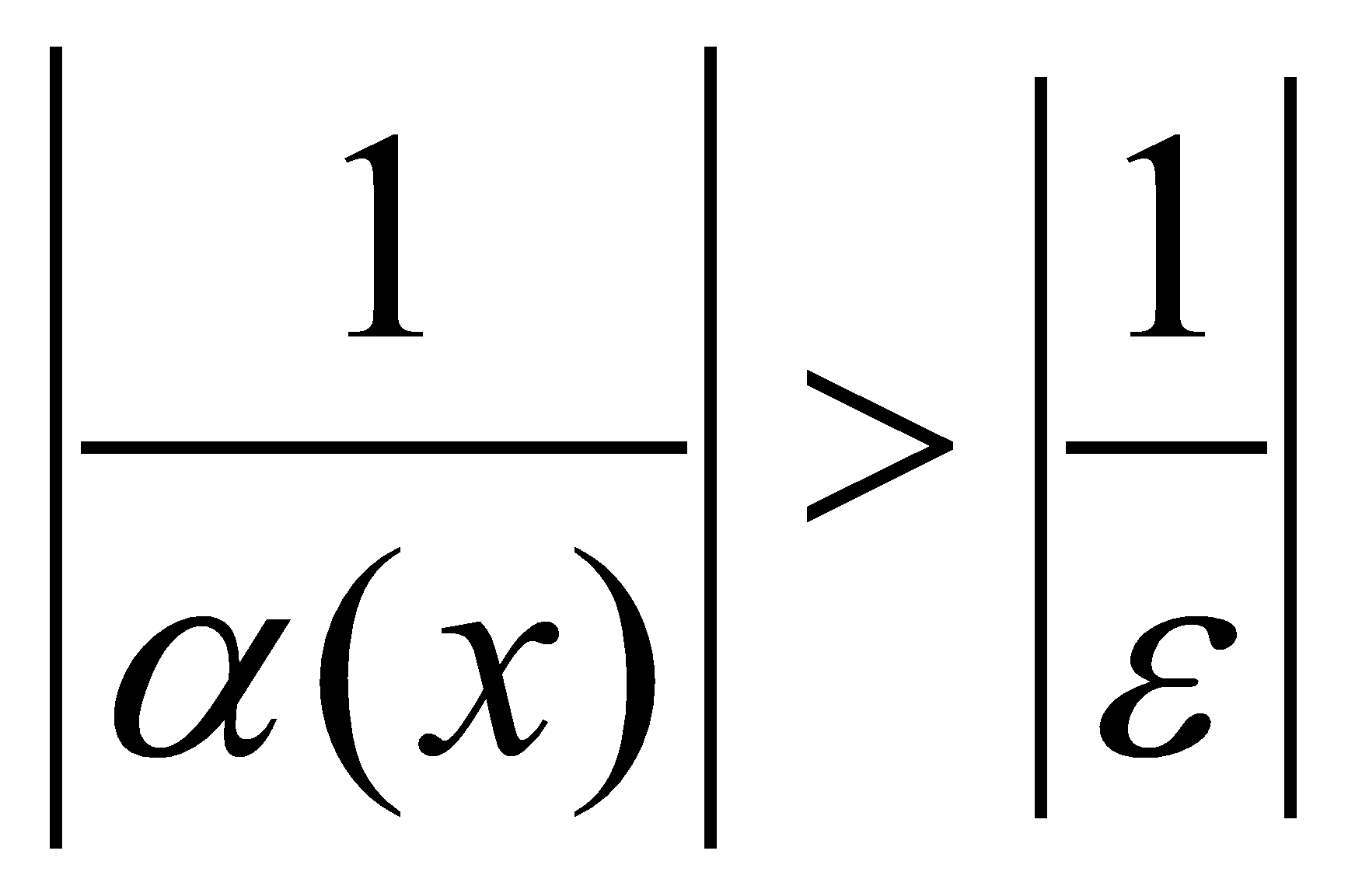, т.е. 
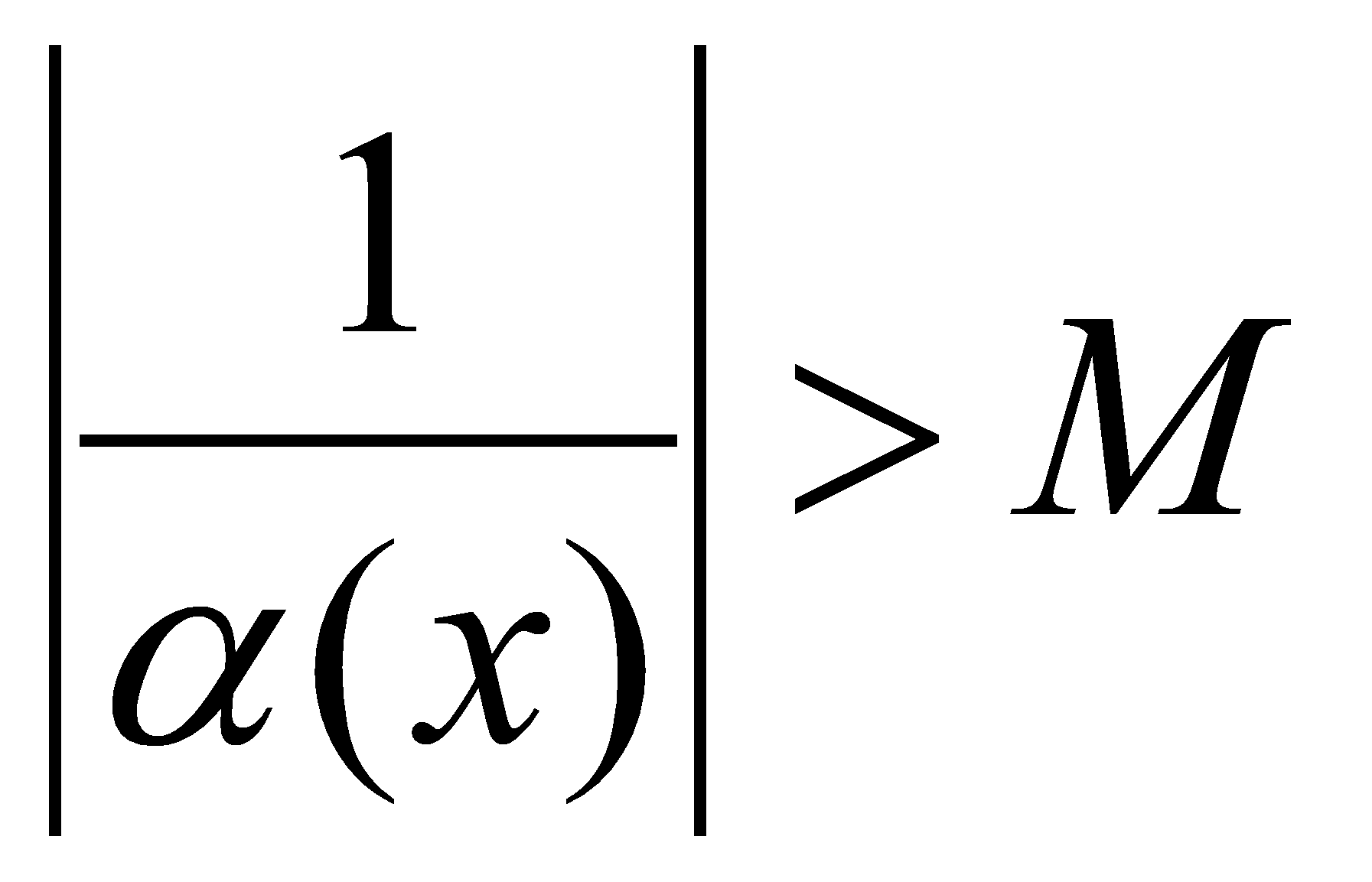, где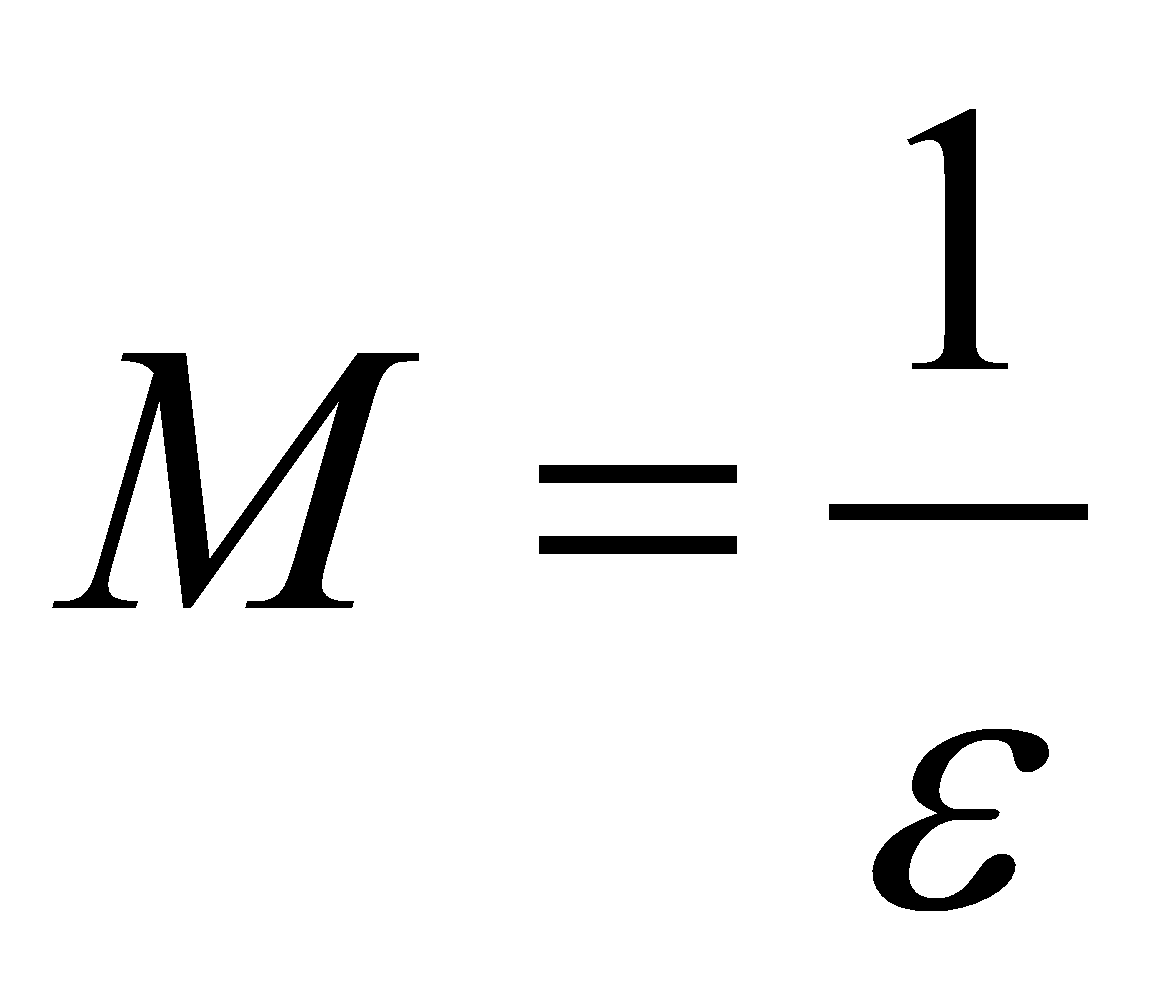 
. А из этого следует, что функция 
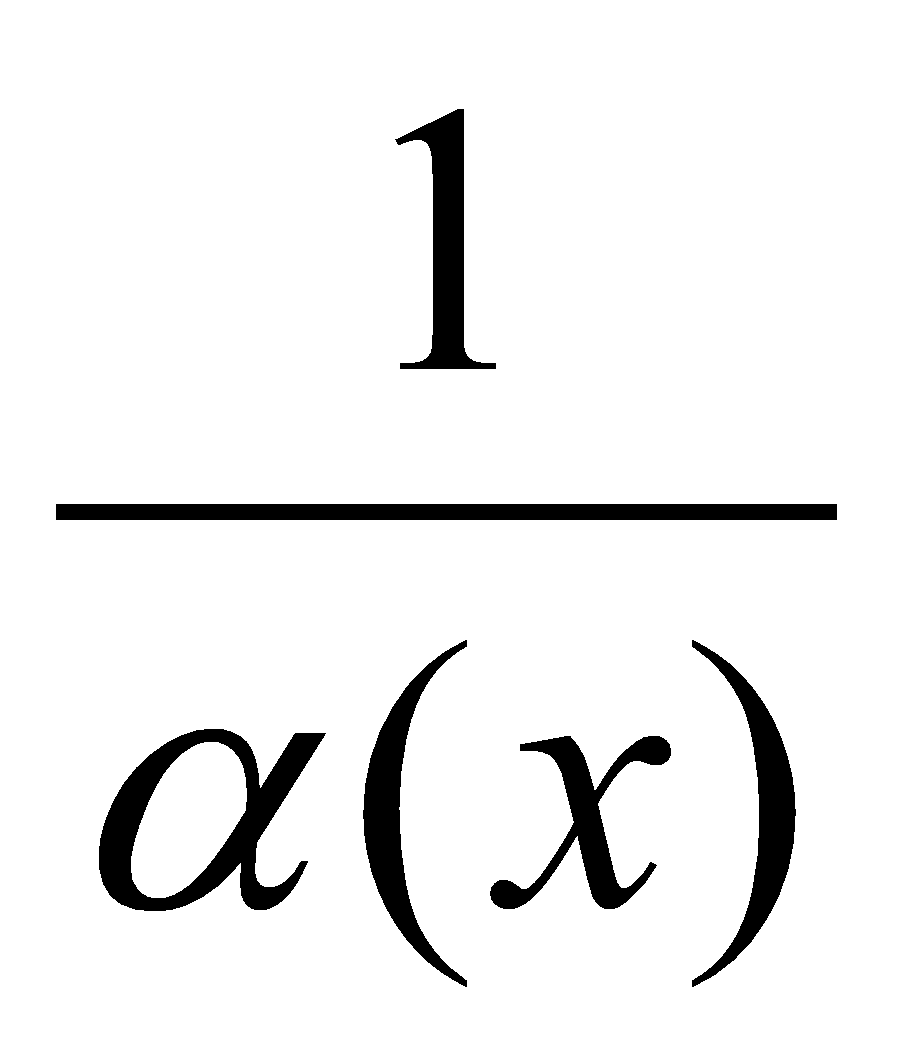- бесконечно большая.
