Рассмотрим систему уравнений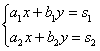 
На первом шаге вычислим определитель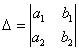 
, его называют главным определителем системы.
Если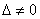 
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
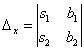и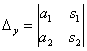 
На практике вышеуказанные определители также могут обозначаться латинской буквой 
.
Корни уравнения находим по формулам: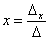
, 
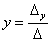
Доказательство теоремы разобъем на три части:
- Решение системы (1) существует и является единственным.
- Равенства (2) являются следствием матричного уравнения (1).
- Равенства (2) влекут за собой матричное уравнение (1).
Так как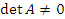 
, то существует и при том единственная, обратная матрица 
.
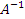Умножая обе части матричного уравнения (1) слева на 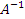, получаем решение этого уравнения:
 |
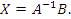(4) |
Единственность обратной матрицы доказывает первую часть теоремы.
Перейдем к доказательству взаимно-однознаяного соответствия между формулами (1) и (2).
Используя формулу (4), получим выражение для i-го элемента. Для этого нужно умножить i-ую строку матрицы
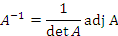
на столбец B.
Учитывая, что i-ая строка присоединенной матрицы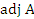 
составлена из алгебраических дополнений 
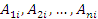, получаем следующий результат:
 |
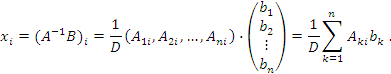(5) |
Сумма в правой части этого равенства представляет собой разложение определителя Di по элементам i-го столбца и, следовательно,
 |
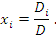(6) |
Вывод формул Крамера завершен. Покажем теперь, что выражения
 |
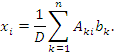(7) |
влекут за собой матричное уравнение (1).
Умножим обе части уравнения (7) на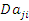 
и выполним суммирование по индексу i:
 |
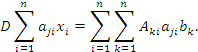(8) |
Изменим порядок суммирования в правой части полученного выражения:
 |
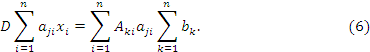(9) |
Согласно Лемме 1,
 |
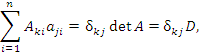(10) |
где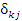 
– дельта символ Кронекера.
Учитывая, что дельта символ 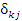снимает суммирование по одному из индексов, получаем требуемый результат:
 |
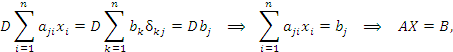